Proof-oriented Programming in F*

fstar-logo

Nik Swamy

Microsoft Research

Oregon Programming Languages Summer School (OPLSS), 2021

Embedding Proof-oriented Programming Languages in F*

fstar-logo

Nik Swamy

Microsoft Research

Oregon Programming Languages Summer School (OPLSS), 2021

Towards High-assurance Software

Through Code Analysis (1)

CompilerWarnings

Through Code Analysis (2)

StaticAnalysis

Program Proofs at Scale

  • Mathematical specifications of correctness and security

  • Machine-checked proof that the code does not deviate from the spec

  • Foundational: Against a formal machine model

  • Integrated: Single theorem covering all the code

  • Many successes in the past 10-15 years

    • CompCert: A certified C compiler in Coq
    • seL4: A verified micro-kernel in Isabelle
    • Ironclad and Ironfleet: Verified distributed systems in Dafny
    • …

Project Everest

https://project-everest.github.io

  • Building and deploying system components with proofs of correctness and security

    • Focusing on secure communication software: TLS, QUIC, Signal, etc.

    • But, also secure sub-systems, like measured boot, high-integrity key-value stores etc.

  • Developed using the F* programming language

  • Building and maintaining formal proofs at scale

    • Multiple times a day, our continuous integration system verifies and builds more than 600,000 lines of F* code and proof

    • Proof automation “in the small”

      • 10^6 small proof obligations discharged by Z3 at each build

      • Domain-specific languages with carefully designed full automation for specific kinds of proofs

    • Modular abstractions to compose proven components

Reusable Verified Artifacts and Tools

Program Proofs in F* for Billions of Unsuspecting Users

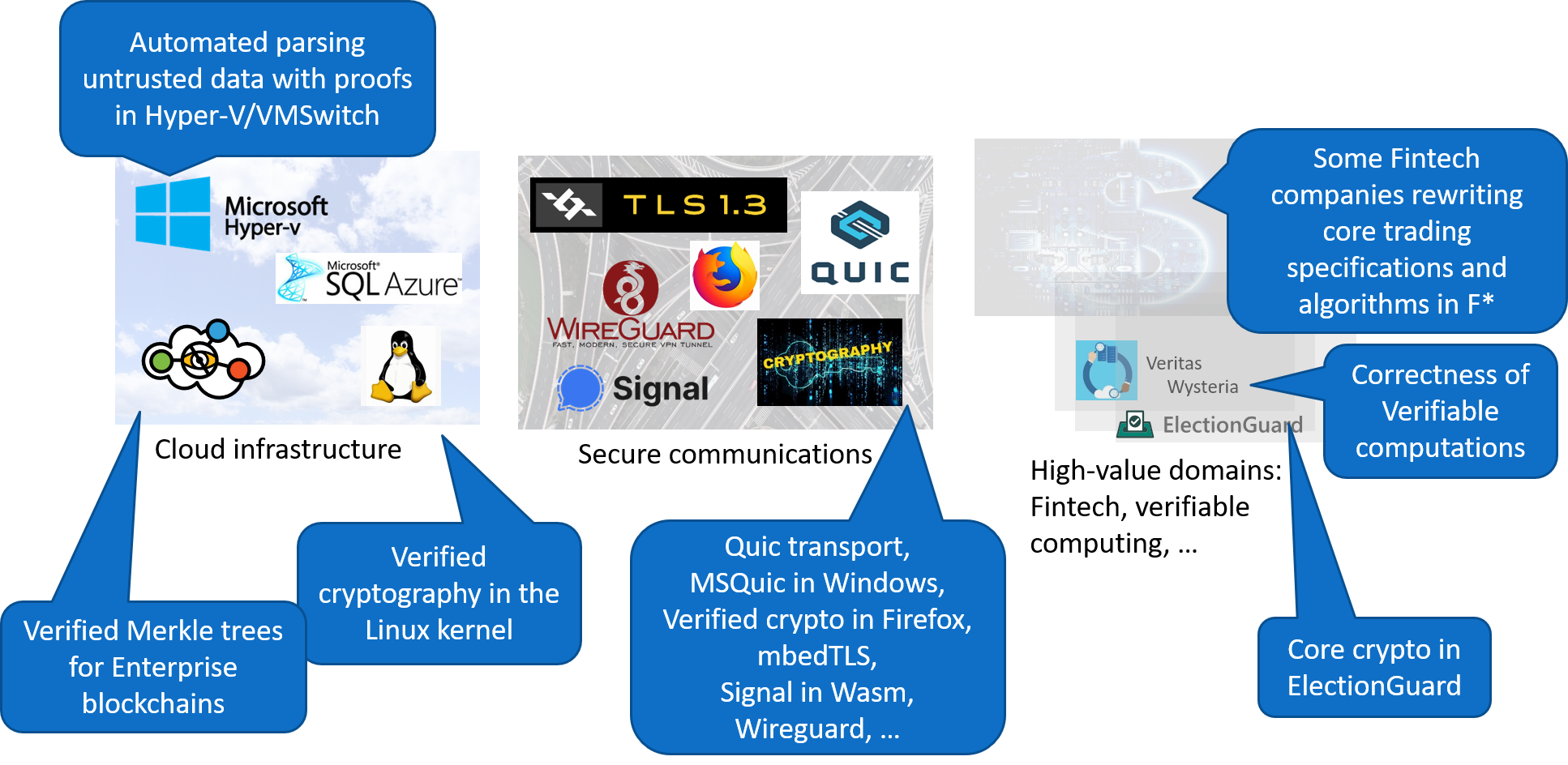
Billions

Contributors (1)

CoreTeam

Contributors (2)

Alumni

Still expensive to develop proofs

  • State of the art: 1 line of code : N lines of manual proof, where

    • N=20, manual, interactive proof of trickiest code
    • N=5, partially automated proofs of imperative code
    • N=0.2, code generated by metaprograms
    • N=0, very specific domains where proofs in specific DSLs can be fully automated

  • Verifying a large piece of existing code, “after the fact”, is still too difficult

  • Often writing a LOT more proof than code

    • Pays to work in a framework optimized for proving and proof automation
    • Pays to structure a program with its proof in mind

Proof-oriented programming

  • Programs and their proofs, co-developed

  • Good synergies:

    • Proofs can be simpler, because the program's structure is designed to facilitate it

    • Programming can be simpler, since proofs guide program construction, e.g., unreachable cases can be ignored

    • Programs can be more “daring”, since invariants help justify optimizations too risky to attempt otherwise

F*: A Framework for Proof-oriented Programming

  • Functional programming language with effects

    • like OCaml, F#, Haskell, …
    • F* extracted to OCaml or F# by default
    • Subset of F* compiled to efficient C code and to Wasm

  • Semi-automated program verifier using automated theorem proving

    • like Dafny, FramaC, Why3, …

  • With an expressive core language based on dependent type theory

    • like Coq, Lean, Agda, Idris, … Nuprl

  • A metaprogramming and tactic framework for interactive proof and user-defined automation

    • like Coq, Isabelle, Lean, PVS, etc.

  • And many foundational program logics for embedded DSLs

    • Many variants of Hoare logic for sequential programs
    • Concurrent separation logic, for concurrent and distributed programs
    • Relational Hoare logic, for program equivalence and security proofs

Proof-oriented Programming Languages Embedded in F*

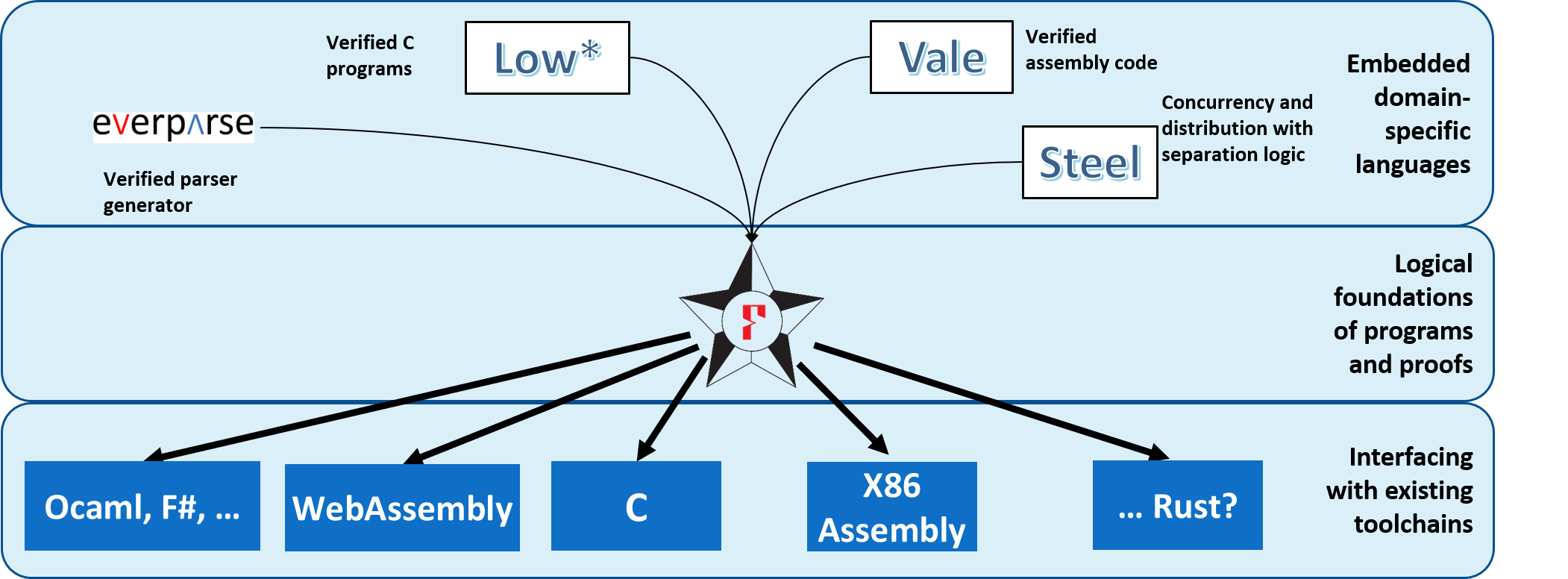
FStar-Arch

Outline of this course

  • Lecture 1: Introducing F*

    • Basic functional programming with dependent types
    • Deep embeddings:
      • Warm up: Simply typed lambda calculus
      • Vale: A proof-oriented assembly language

  • Lecture 2: Shallow embeddings of effectful languages

    • Stateful programming with an ML-style heap
    • Indexed computations and Dijkstra monads
    • Security-oriented programming: An embedded language with information flow control

Outline of this course

  • Lecture 3: Layering effectful DSLs

    • Low*: Programming and proving with a C-like memory model
    • EverParse: A parser generator layered on Low*

  • Lecture 4: Concurrent programming and separation logic

    • Warm up: A total semantics for concurrency
    • Deriving a concurrent separation logic for partial correctness
    • Steel: A DSL for proof-oriented concurrent and distributed programming

Installing F*

F* Interactive Mode in Emacs

https://github.com/FStarLang/fstar-mode.el

Resources to learn more about F*

https://fstar-lang.org

Today: Dependently typed functional programming in F*

Basic types

  • The empty type: It has no values 

    type empty =

  • The singleton: It has exactly 1 value 

    type unit = ()

  • Boolean: It has exactly 2 values 

    type bool = true | false

  • …

Inductive type definitions

  • Simple inductive data types 
type list a =
  | Nil : list a
  | Cons : hd:a -> tl:list a -> list a
  • But, actually, (mutually) inductive type families 
type rbtree a : nat -> color -> Type =
  | Leaf : rbtree a 1 Black
  | R    : left:rbtree a h Black -> value:a -> right:rbtree a h Black -> rbtree a h Red
  | B    : left:rbtree a h cl -> value:a -> right:rbtree a h cr -> rbtree a (h+1) Black

Recursive functions

  • Recursive functions 

    let rec factorial (n:int) : int =
    if n = 0 then 1 else n * (factorial (n - 1))

  • Inductive datatypes (immutable) and pattern matching 

    let rec map (f: a -> b) (x:list a) : list b =
  match x with
  | [] -> []
  | hd :: tl -> f hd :: map f tl

  • Lambdas (unnamed, first-class functions) 

    map (fun x -> x + 42) [1;2;3] ~> [43;44;45]

Refinement types

type nat = x:int{x>=0}

  • Informal mental model: A type describes a set of values 

    let empty = x:int { false } //one type for the empty set
let zero = x:int{ x = 0 } //the type containing one element `0`
let pos = x:int { x > 0 } //the positive numbers
let neg = x:int { x < 0 } //the negative numbers
let even = x:int { x % 2 = 0 } //the even numbers
let odd = x:int { x % 2 = 1 } //the odd numbers
let prime = x:nat { forall n. x % n = 0 ==> n = 1 || n = x } //prime numbers

  • Refinements introduced by type annotations (code unchanged) 

    let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1))

  • Logical obligations discharged by SMT (simplified) 

    n >= 0, n <> 0 |= n - 1 >= 0
n >= 0, n <> 0, factorial (n - 1) >= 0 |= n * (factorial (n - 1)) >= 0

  • Refinements eliminated by subtyping: nat<:int 

    let i : int = factorial 42
let f : x:nat{x>0} -> int = factorial

Dependent types

  • Dependent function types ($\Pi$), here together with refinements: 

    val incr : x:int -> y:int{x < y}
let incr x = x + 1

  • Can express pre- and post- conditions of pure functions 

    val incr : x:int -> y:int{y = x + 1}

  • Exercise: Can you find other types for incr?

Total, recursive functions

  • Tot effect (default) = no side-effects, terminates on all inputs 

    let rec factorial (n:nat) : nat = (if n = 0 then 1 else n * (factorial (n - 1)))

  • F* refuses to accept this type for factorial. Why? 

    val factorial : int -> int
  let rec factorial n = (if n = 0 then 1 else n * (factorial (n - 1)))
                                                              ^^^^^
  Subtyping check failed; expected type (x:int{x << n}); got type int

factorial (-1) loops! (int type in F* is unbounded)

Semantic termination checking

  • based on well-founded ordering on expressions (<<)

    • naturals related by < (negative integers unrelated)
    • inductives related by subterm ordering
      • x << D x
      • f x << D f
    • lexicographic tuples %[a;b]
      • %[a; b] << [a'; b'] if a << a', or a = a' and b << b'
      • Derived from the subterm ordering using accessibility predicates

  • arbitrary total expression as decreases metric 

    val ackermann: m:nat -> n:nat -> Tot nat (decreases %[m;n])
let rec ackermann (m n:nat)
  : Tot nat (decreases %[m;n])
  = if m=0 then n + 1
    else if n = 0 then ackermann (m - 1) 1
    else ackermann (m - 1) (ackermann m (n - 1))

  • default metric is lex ordering of all (non-function) args 

    val ackermann: m:nat -> n:nat -> Tot nat

Lemmas

let rec length (xs:list a) : nat =
  match xs with
  | [] -> 0
  | _::tl -> 1 + length tl

let rec append (xs ys : list a) : list a =
  match xs with
  | [] -> ys
  | x :: xs' -> x :: append xs' ys
  • Prove that the length of append is the sum of the lengths of its arguments 
    let rec append_length (xs ys : list a) : Lemma (length (append xs ys) = length xs + length ys)
    = match xs with
      | [] -> ()
      | x :: xs' -> append_length xs' ys
    • Proof by induction on xs
      • Base case, xs=[] is easy: append [] ys = ys /\ length [] = 0
      • Step: Use IH by calling function recursively on smaller arguments
      • Sugar: Lemma p = u:unit { p } `

More Lemmas

let snoc l h = l @ [h]

let rec reverse (l:list a) : list a =
  match l with
  | [] -> []
  | hd::tl -> snoc (reverse tl) hd
let rec rev_snoc (l:list a) (h:a)
  : Lemma (reverse (snoc l h) == h::reverse l)
  = match l with
    | [] -> ()
    | hd::tl -> rev_snoc tl h
let rec rev_involutive (l:list a)
  : Lemma (reverse (reverse l) == l)
  = match l with
    | [] -> ()
    | hd::tl -> rev_involutive tl; rev_snoc (reverse tl) hd

Proof of a program: QUICKSORT

  • Work through the online tutorial and you'll reach eventually a proof of correctness of quicksort. 
let rec quicksort (f:total_order a) (l:list a)
  : Tot (m:list a{sorted f m /\ is_permutation l m})
        (decreases (length l))
  = match l with
    | [] -> []
    | pivot::tl ->
      let hi, lo = partition (f pivot) tl in
      let m = quicksort f lo @ pivot :: quicksort f hi in
      permutation_app_lemma pivot tl (quicksort f lo) (quicksort f hi);
      m

Demo: Two Deeply Embedded Languages

  • Basics: factorial, lemmas, vectors

  • Warm up: Simply Typed Lambda Calculus

  • Vale: A Proof-oriented Assembly Language

Extra

Lemmas, squashed types, and proof irrelevance

  • Lemma p is sugar for Tot (u:unit{p})

  • We write squash p instead of u:unit{p}

    • So, Lemma p is sugar for Tot (squash p)

  • The type squash p is a sub-singleton, i.e., it has at most one element (). 

(** All proofs of [squash p] are equal  *)
val proof_irrelevance (p: Type) (x y: squash p) : Tot (squash (x == y))

  • The type prop in F* is defined as all the subtypes of unit.

    • i.e., For p:prop and proof of p, i.e., e:p is noninformative

Equality

  • Two notions of equality

  • Definitional equality: $e_1 \equiv e_2$ if and only if $\exists e. e_1 \leadsto^{*} e \wedge e_2 \leadsto^{*} e$.

  • Provable equality: $e_1$ and $e_2$ are provably equal if $equals~e_1~e_2$ is inhabited, i.e., you can build a term of the following type 

type equals (#a: Type) (x: a) : a -> Type = | Refl : equals x x
  • In F*, we write x == y to mean squash (equals x y).

Extensionality: The Essence of F*

  • Clearly, if x $\equiv$ y then x == y.

  • In intensional type theories, given e : t and t $\equiv$ t', then by conversion e : t'.

  • Equality reflection: In F*, like in other extensional type theories (e.g., Nuprl), if e:t and t == t', then e : t'.

    • i.e., types conversion is possible through the silent use of provable equalities

    • v: vec a (n + 0) is convertible with vec a n, since (n + 0) == n, although n + 0 $\not\equiv$ n.

  • However, this makes typechecking in F* undecidable

    • Practically speaking, F* uses SMT to decide if/when a conversion is applicable

Functional Extensionality, Subtyping and Eta reduction

  • With equality reflection, it is possible to prove, when `e == e': 

    (fun (x:a) -> e) == (fun (x:a) -> e')

  • But, subtyping adds another level of subtletly (we got this wrong a couple of times)

  • Due to refinement subtyping, we have (x:t0 -> t0') <: (x:t1 -> t1') when t1 <: t0 and t0' <: t1'.

    • E.g., (int -> nat) <: (nat -> int).

  • But, this means that eta reductions do not preserve types

    • E.g., for f:int -> nat, reducing fun (x:nat) -> f x to f widens its domain.

  • Given some f, g: int -> nat, proving equals (fun (x:nat) -> f x) (fun (x:nat) -> g x) does not imply equals f g (e.g., we may have f (-1) <> g (-1)).

  • So, definitional equality in F* does not include eta reduction