Verifying Low-level Code for Security and Correctness using F*
Program verification: Shall the twain ever meet?
| Interactive proof assistants | Semi-automated verifiers of imperative programs | |||
|---|---|---|---|---|
| Coq, | CompCert, | air | Dafny, | Verve, |
| Isabelle, | seL4, | FramaC, | IronClad, | |
| Agda, | Bedrock, | Why3 | miTLS | |
| Lean, Nuprl, … | 4 colors | gap | Vale | |
-
In the left corner: Very expressive dependently-typed logics,
but only purely functional programming -
In the right: effectful programming, SMT-based automation,
but only first-order logic
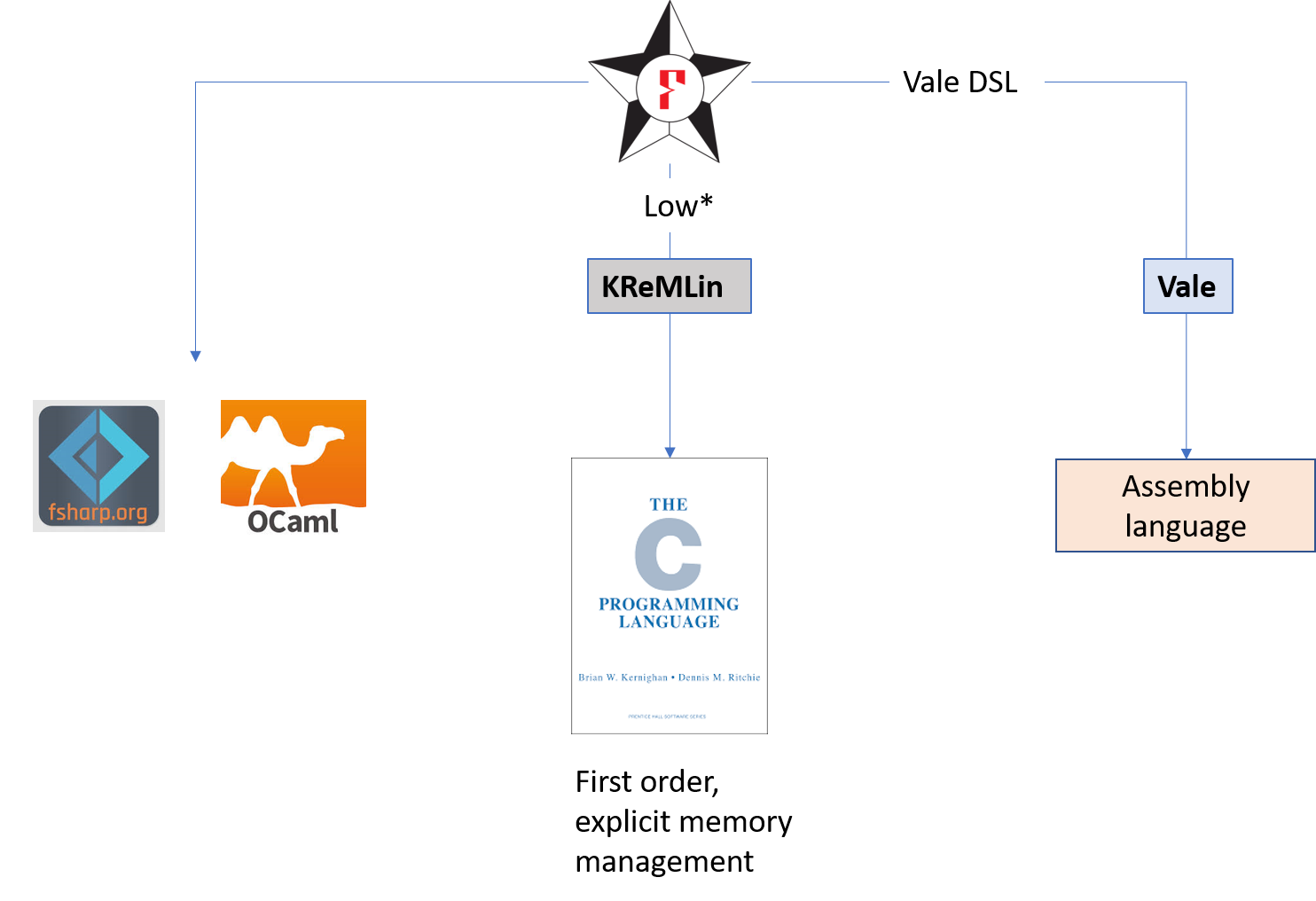
Bridging the gap: F*
-
Functional programming language with effects
- like OCaml, F#, Haskell, …
- F* extracted to OCaml or F# by default
- Subset of F* compiled to efficient C code
-
Semi-automated verification system using SMT
- like Dafny, FramaC, Why3, …
-
With an expressive core language based on dependent type theory
- like Coq, Lean, Agda, Nuprl, …
-
A metaprogramming and tactic framework for interactive proof and user-defined automation
- like Coq, Isabelle, Lean, Nuprl, etc.
A first taste
-
Write ML-like code
let rec factorial n = if n = 0 then 1 else n * factorial (n - 1) -
Give it a specification, claiming that
factorialis a total function from non-negative to positive integers.val factorial: n:int{n >= 0} -> i:int{i >= 1} -
Ask F* to check it
fstar factorial.fst Verified module: Factorial All verification conditions discharged successfully
fstar factorial.fst
Verified module: Factorial
All verification conditions discharged successfullyF* builds a typing derivation of the form:
-
In a context including definitions of F* primitives
-
The program has type , given the validity of a logical formula
-
is passed to Z3 (an automated theorem prover/SMT solver) to check for validity
-
If the check succeds, then, from the metatheory of F*, the program is safe at type
Running F* Programs
Some uses of F*
- Project Everest: verify and deploy new, efficient HTTPS stack
- Verified Everest code deployed in
- Firefox (Mozilla NSS crypto)
- Windows (WinQUIC)
- Azure Confidential Consortium (Verified Merkle tree for the blockchain)
- WireGuard VPN
- Zinc crypto library for Linux
- Tezos and Concordium blockchains
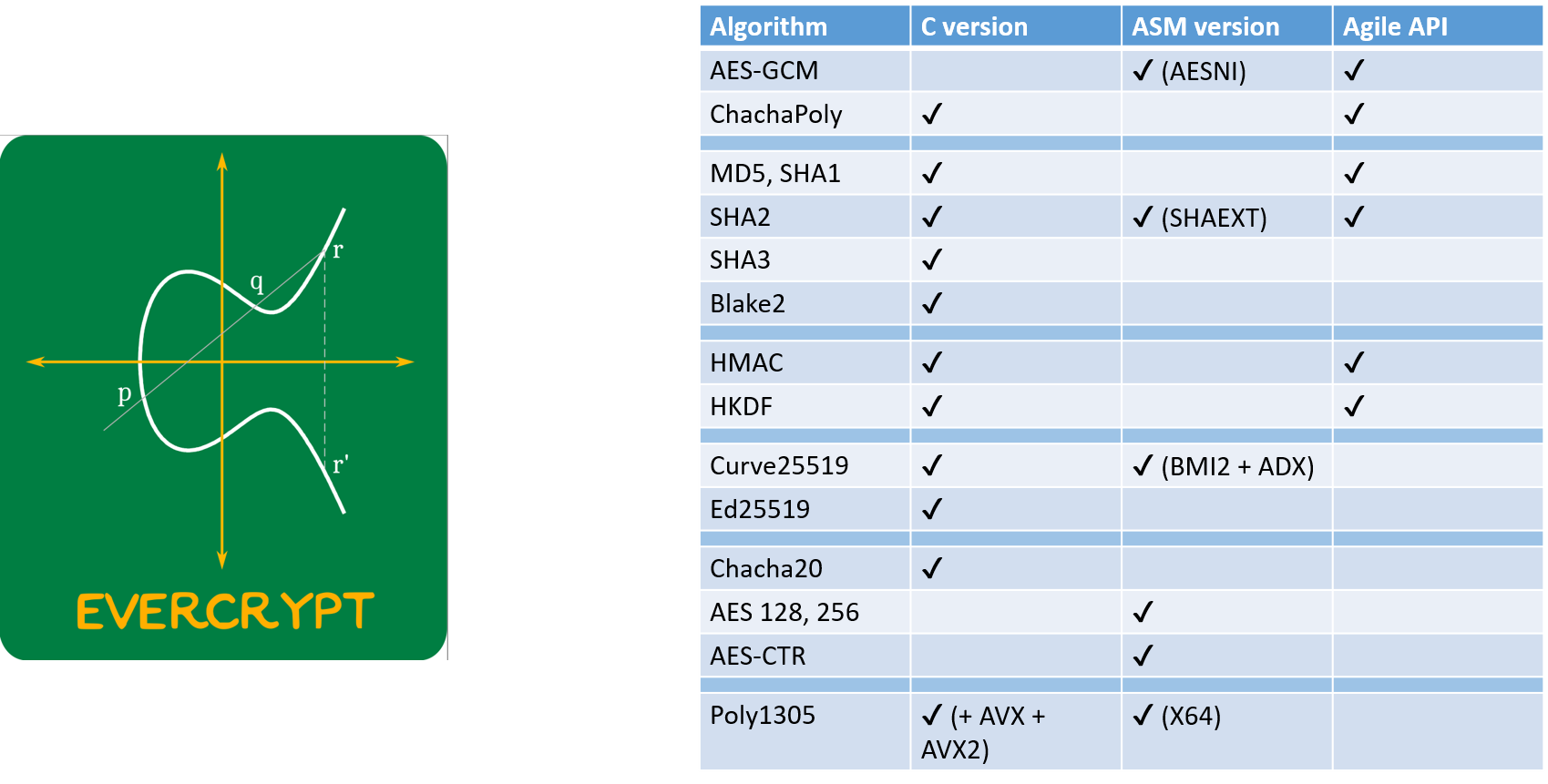
EverCrypt: A No-Excuses, Verified Cryptographic Provider
- 180KLOC of code & proof, producing 40KLOC of verified C & assembly
- Memory safe
- Functionally correct
- Side-channel resistant
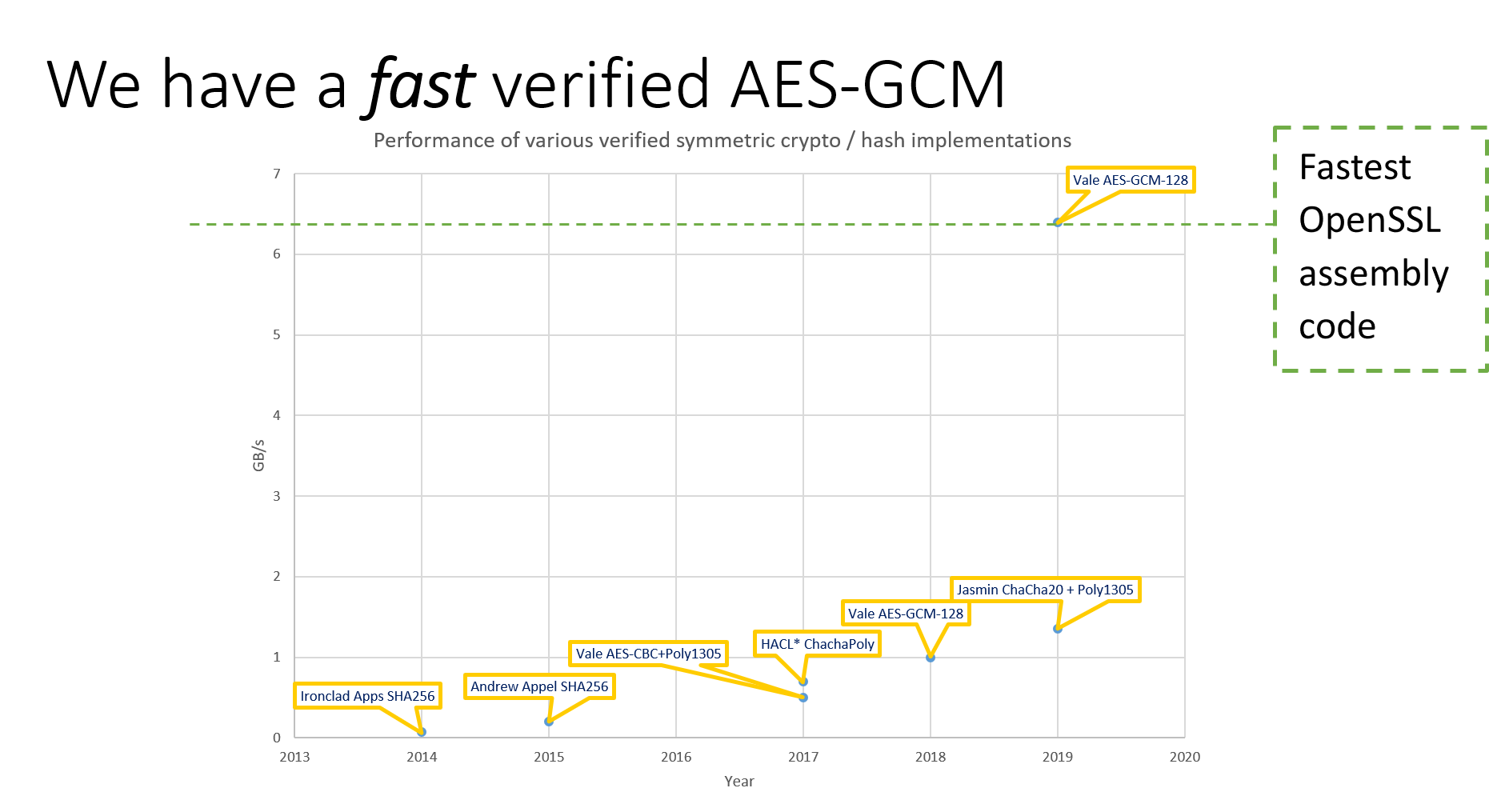
AES-GCM: Authenticated Encryption for 90% of Secure Internet Traffic
The Current Everest and F* team
Microsoft Research, Inria Paris, CMU, MIT, Rosario, …
- many former members, interns, external contributors, … you?
This talk
-
Need to write low-level code for performance
- Cryptographic routines are heavily optimized in C and assembly
- Networking protocols are inherently effectful
-
Need to write low-level code for security
- Hard to control side-channels with a GC, JIT etc.
-
Specifying and verifying effectful programs is hard
-
Much effort involved in designing and structuring specifications, perhaps more effort than programming effectful code itself
-
Typical code to proof ratio for functional correctness and security proofs is ~ 1 : 5 (more like 1 : 20 without SMT)
-
-
Pays to structure specifications well … functional programming can help
Computations indexed by familiar FP structures
Core F* design principle:
-
Computation types are indexed by their specifications
- Specs equipped with some algebraic structure for formal manipulation
Three examples:
-
Weakest precondition inference: Monads indexed by WP-monads
-
Imperative data access code: Lens-indexed imperative lenses
-
Low-level parsers: Parser-indexed imperative parsers
- Low-level formatters: Indexed by parsers, their inverses
-
… many more structures still to be discovered
Later this week
- Modeling and proving cryptographic security
- Implementing efficient, verified cryptographic algorithms in Low* (C)
- Faster, lower, still correct & secure: Verified assembly programs (Vale)?
- Relational equivalences in F*?
Try the tutorial: https://fstar-lang.org/tutorial
- New release just for you!
- v0.9.7.0-alpha1 (Summer Schools)
- https://github.com/FStarLang/FStar/releases
The Functional Core of F*
Informally, like Coq or Agda, but with an extensional type theory (~Nuprl)
-
Refinement types
let nat = x:int{x>=0} -
Recursive functions
let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1))
Refinement types
type nat = x:int{x>=0}-
Refinements introduced by type annotations (code unchanged)
let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1)) -
Logical obligations discharged by SMT (simplified)
n >= 0, n <> 0 |= n - 1 >= 0 n >= 0, n <> 0, factorial (n - 1) >= 0 |= n * (factorial (n - 1)) >= 0 -
Refinements eliminated by subtyping:
nat<:intlet i : int = factorial 42 let f : x:nat{x>0} -> int = factorial
Dependent types
-
Dependent function types (), here together with refinements:
val incr : x:int -> y:int{x < y} let incr x = x + 1 -
Can express pre- and post- conditions of pure functions
val incr : x:int -> y:int{y = x + 1} -
Exercise: Can you find other types for
incr?
Inductive types and pattern matching
-
Inductive datatypes (immutable) and pattern matching
type list a = | Nil : list a | Cons : hd:a -> tl:list a -> list a let rec map (f:a -> b) (x:list a) : list b = match x with | [] -> [] | h :: t -> f h :: map f t -
Lambdas (unnamed, first-class functions)
map (fun x -> x + 42) [1;2;3]
Inductive types and pattern matching
-
Recursive functions over inductive datatypes
type vec a : nat -> Type = | Nil : vec a 0 | Cons : #n:nat -> hd:a -> tl:vec a n -> vec a (n + 1) let rec append (v1:vec a n) (v2:vec a m) : vec a (n + m) = match v1 with | Nil -> v2 | Cons hd tl -> Cons hd (append tl v2) -
Higher order
let rec map (f:a -> b) (v:vec a n) : vec b n = match v with | Nil -> Nil | Cons hd tl -> Cons (f hd) (map f tl) map (fun x -> x + 42) (Cons 1 Nil)
Total functions in F*
-
The F* functions we saw so far were all total
-
Toteffect (default) = no side-effects, terminates on all inputsa -> bis really shorthand fora -> Tot b
val factorial : nat -> nat ~ nat -> Tot nat let rec factorial n = (if n = 0 then 1 else n * (factorial (n - 1))) -
Quiz: How about giving this weak type to factorial?
val factorial : int -> Tot int
let rec factorial n = (if n = 0 then 1 else n * (factorial (n - 1)))
^^^^^
Subtyping check failed; expected type (x:int{(x << n)}); got type int factorial (-1) loops! (int type in F* is unbounded)
Semantic termination checking
- Based on well-founded ordering on expressions (
<<)- naturals related by
<(negative integers unrelated) - inductives related by subterm ordering
- lex tuples
%[a;b;c]with lexicographic ordering - result of a total function smaller than the function itself (
f x << f)
- naturals related by
- order constraints discharged by the SMT solver
- arbitrary total expression as decreases metric
let rec ackermann (m n:nat) : Tot nat (decreases %[m;n]) = if m=0 then n + 1 else if n = 0 then ackermann (m - 1) 1 else ackermann (m - 1) (ackermann m (n - 1)) - default metric is lex ordering of all (non-function) args
val ackermann: m:nat -> n:nat -> Tot nat
Values and Computations
-
“Values” aka unconditionally total terms
-
Two classes of types
- Value types (
t):int,list int, … - Computation types (
C): conditionally pure, divergent, stateful, …
- Value types (
-
F* effect system encapsulates effectful code
- Pure code cannot call effectful code
- But, via sub-effecting, pure code can be used in effectful contexts
-
Dependent function types of the form:
x:t -> C- F* is call-by-value
- argument can't have side-effects, so value type
-
Two forms of refinement types
- Refined value types:
x:t{p} - Refined computation types …
- Refined value types:
Refined Computation Types
Monadic effects in F*
- A classic state monad:
type st a = s -> (a * s)
let return x h = x,h
let bind f g h = let x,h' = f h in g x h'
let get () h = h,h
let put h _ = (),h-
Turned into an abstract “computation type” and can be primitively implemented under the hood or not
new_effect STATE { st; return; bind; get; put } -
Can now program effectful computations directly:
let double () = put (get () + get ()) -
And F* infers
double : unit -> STATE unit w
Specifying Effectful Programs
-
Type inference in F* includes inference of weakest preconditions
-
e : STATE a wmeansforall post h0. //for all postconditions and initial states w post h0 ==> //given the weakest precondition is valid for post and h0 e h0 ~>* (v, h1) /\ //the computation reduces to a value and final state post (v, h1) //that validate the postcondition -
What is a weakest precondition predicate transformer?
let st_wp a : st_post a -> st_pre //transforms postconditions to preconditions where st_post a : (a * s) -> prop //postconditions relate results to memories and st_pre : s -> prop //preconditions are memory predicates -
Dijkstra monad for state
WP inference CPS tranform
let st_wp a : st_post a -> st_pre //transforms postconditions to preconditions
where st_post a : (a * s) -> prop //postconditions relate results to memories
and st_pre : s -> prop //preconditions are memory predicates- Hey, wait a minute … isn't that like the continuation monad?
cont r a = (a -> r) -> r-
Take the continuation monad with result type
props -> cont prop (a * s) = s -> ((a * s) -> prop) -> prop ~ ((a * s) -> prop) -> s -> prop = st_post a -> st_pre = st_wp a -
WPs for state are just the state monad transformer applied to the continuation monad with result type
propstateT m a = s -> m (a * s) st_wp a = stateT (cont prop) a
Auto-generating WP calculi for monads
-
F* automatically derives a weakest precondition calculus for m-effectful computations whose WPs have the form
m_wp a = mT (cont prop) a- the
mtransformer on the continuation monad with result typeprop
- the
-
And infers computations types of the form
M a (wp : m_wp a) -
E.g., for exceptions
ex_wp a = ex_t (cont prop) a = (option a -> prop) -> prop -
For state + exceptions
st_ex_wp a = state_t (ex_t (cont prop)) a = s -> (ex_t (cont prop) a * s) = s -> ((option a * state) -> prop) -> prop ~ ((option a * state) -> prop) -> s -> prop = st_ex_post a -> st_ex_pre
Derived Specifications: Hoare triples
-
Reasoning about continuations: great for a core logic / not for a human
-
Hoare logic-style pre-conditions and post-conditions
ST a (pre: s -> prop) (post: s -> a -> s -> prop) = STATE a (fun k s0 -> pre s0 /\ (forall x s1. post s0 x s1 ==> k (x, s1))) -
stateful pre-condition is predicate on initial states
-
post-condition is relation on initial states, results, and final states
val get ()
: ST s
(requires fun s -> True)
(ensures fun s0 result s1 -> s0 == result /\ result == s1)
val put s
: ST unit
(requires fun _ -> True)
(ensures fun _ _ s1 -> s1 == s0)Richer Model of Mutable Memory
with Lens-indexed Imperative Lenses
Richer memory models
-
Program libraries to model memory, e.g., the ML heap
-
Derive effectful actions for primitive operations (e.g.,
!,:=etc.) -
Write effectful programs against these libraries and verify them with refined computation types
-
Extract them to programs in ML or C with primtive effects
-
F*:
let incr (r:ref int) : ST unit (requires (fun _ -> True)) (ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\ sel h2 r = sel h1 r + 1)) = r := !r + 1ML:
let incr (r:ref int) : unit = r := !r + 1C:
void incr (int *r) { *r = *r + 1; }
Modeling the ML heap
A sketch of FStar.Heap:
module Heap
let addr = nat
abstract let heap = {
next_addr: addr;
map: addr -> option (a:Type & v:a) {
forall a. h > next_addr ==> map a == None
}
}
abstract let ref t = addr
let contains h (r:ref t) = r < h.next_addr /\ h.map r == Some (t, _)
let sel h (r:ref t{h `contains` r}) = let Some (_, v) = h.map r in v
let upd h (r:ref t{h `contains` r}) v = ...
Deriving ML-like Effectful Operations
-
Reading references
let (!) #t (r:ref t) : ST t (requires fun h -> h `contains` r) (ensures fun h0 x h1 -> h0 == h1 /\ x = sel h1 r) = sel (get()) r -
Writing references
let (:=) #t (r:ref t) (v:t) : ST (ref t) (requires fun h -> h `contains` r) (ensures fun h0 x h1 -> h1 == upd h0 r v) = put (upd (get()) r v); r -
Allocating and freeing references …
Freeing references
let free #r (r:ref t)
: ST unit
(requires fun h -> h `contains` r)
(ensures fun h0 () h1 -> modifies !{r} h0 h1)
= let h = get () in
put ({h with map = fun a -> if a = r then None else h.map a})Bidirectional data access, abstractly with lenses
type lens a b = {
get : a -> b;
put : b -> a -> a
}selandupdform a lenslet ref_lens : lens (heap * ref a) a = { get = fun (h, r) -> sel h r; put = fun v (h, r) -> upd h r v }
Imperative lenses
-
A lens-indexed computation type:
type st_lens inv (l:lens (heap * a) b) = { st_get : x:a -> ST b (requires fun h -> inv h x) (ensures fun h0 y h1 -> h0==h1 /\ y == l.get (h0, x)); st_put : y:b -> x:a -> ST a (requires fun h -> inv h x) (ensures fun h0 x' h1 -> h1, x' == l.put y (h0, x)) } -
(!) and (:=) are imperative lenses
let iref_lens : st_lens contains ref_lens = { st_get = (!); st_put = (:=); }
Manipulating Binary-formatted Data
with the EverParse parser combinator library
Networking Protocols: Many performance and security-critical parsers
-
TLS 1.3 message format, with variable-length data
uint16 ProtocolVersion; opaque Random[32]; uint8 CipherSuite[2]; struct { ProtocolVersion legacy_version = 0x0303; Random random; opaque legacy_session_id<0..32>; CipherSuite cipher_suites<2..2^16-2>; opaque legacy_compression_methods<1..2^8-1>; Extension extensions<8..2^16-1>; } ClientHello; -
De facto: Hand-written parsers and formatters, for performance, but also many vulnerabilities
- Heartbleed was a parsing bug
EverParse: A Verified Low-level Parser Generator
-
Given a type description (e.g., ClientHello)
-
Produces a parser and a formatter indexed by its (inverse) parser
let parser t = b:bytes -> option (t * n:nat{n <= length b})
let format (p:parser t) = f:(t -> bytes) {
forall x. p (f x) == Some (x, length (f x))
}- And a low-level zero-copy validator indexed by the parser
let validator (p:parser t) = bs:array uint8 -> pos:u32 { pos <= length bs } -> ST u32 (requires fun h0 -> h0 `contains` bs) (ensures fun h0 res h1 -> h0 == h1 /\ (if res < ERROR_CODE then exists v. p (as_bytes bs h0 pos) = Some (v, res) (* parsing succeeds *) else p (as_bytes bs h0 pos) = None (* parsing fails *)))
Combinator library for validators
- Mirroring the structure of parser combinators
val return : validator unit_parser
val bind : validator p -> (t -> validator q) -> validator (p `Parser.bind` q)
val seq: validator p -> validator s -> validator (p `Parser.seq` s)
val map : f:(t -> s) -> validator p -> -> validator (Parser.map f p)
...-
Client-hello validator
protocolVersion_validator `seq` random_validator `seq` sessionID_validator `seq` clientHello_cipher_suites_validator `seq` clientHello_compression_method_validator `seq` clientHelloExtensions_validator -
Imperative code refines pure parser by construction
Data accessors
-
Structured access into validated binary data, specified by parsers and lenses
let accessor (p1:parser t1) (p2:parser t2) (l:lens t1 t2) = bs:array uint8 -> pos:u32 { pos <= length bs } -> ST u32 (requires fun h0 -> h0 `contains` bs /\ Some? (p1 (as_bytes bs h0 pos))) (* bs contains a valid t1 *)) (ensures fun h0 res h1 -> h0 == h1 /\ let Some (v1, _) = p1 (as_bytes bs h0 pos) in p2 (as_bytes bs h0 res) == Some (l.get v1, _)) (* returns offset to t2 *) -
Abstractly, structured data access into a (representation of)
t1 -
Concretely, just performs arithmetic into the binary formatted data
- Effectively, reads directly from computed offsets into network packets
- Would be crazy to try this directly in C!
Extracted to efficient C code
- After partial evaluation and proof erasure …
uint32_t Parsers_ClientHello_clientHello_validator(LowParse_Low_Base_slice input, uint32_t pos)
{
uint32_t pos10 = Parsers_ProtocolVersion_protocolVersion_validator(input, pos);
uint32_t pos11;
if (pos10 > ERROR_CODE)
pos11 = pos10;
else
pos11 = Parsers_Random_random_validator(input, pos10);
uint32_t pos12;
if (pos11 > ERROR_CODE)
pos12 = pos11;
else
pos12 = Parsers_SessionID_sessionID_validator(input, pos11);
uint32_t pos13;
if (pos12 > ERROR_CODE)
pos13 = pos12;
else
pos13 = Parsers_ClientHello_cipher_suites_clientHello_cipher_suites_validator(input, pos12);
uint32_t pos1;
...
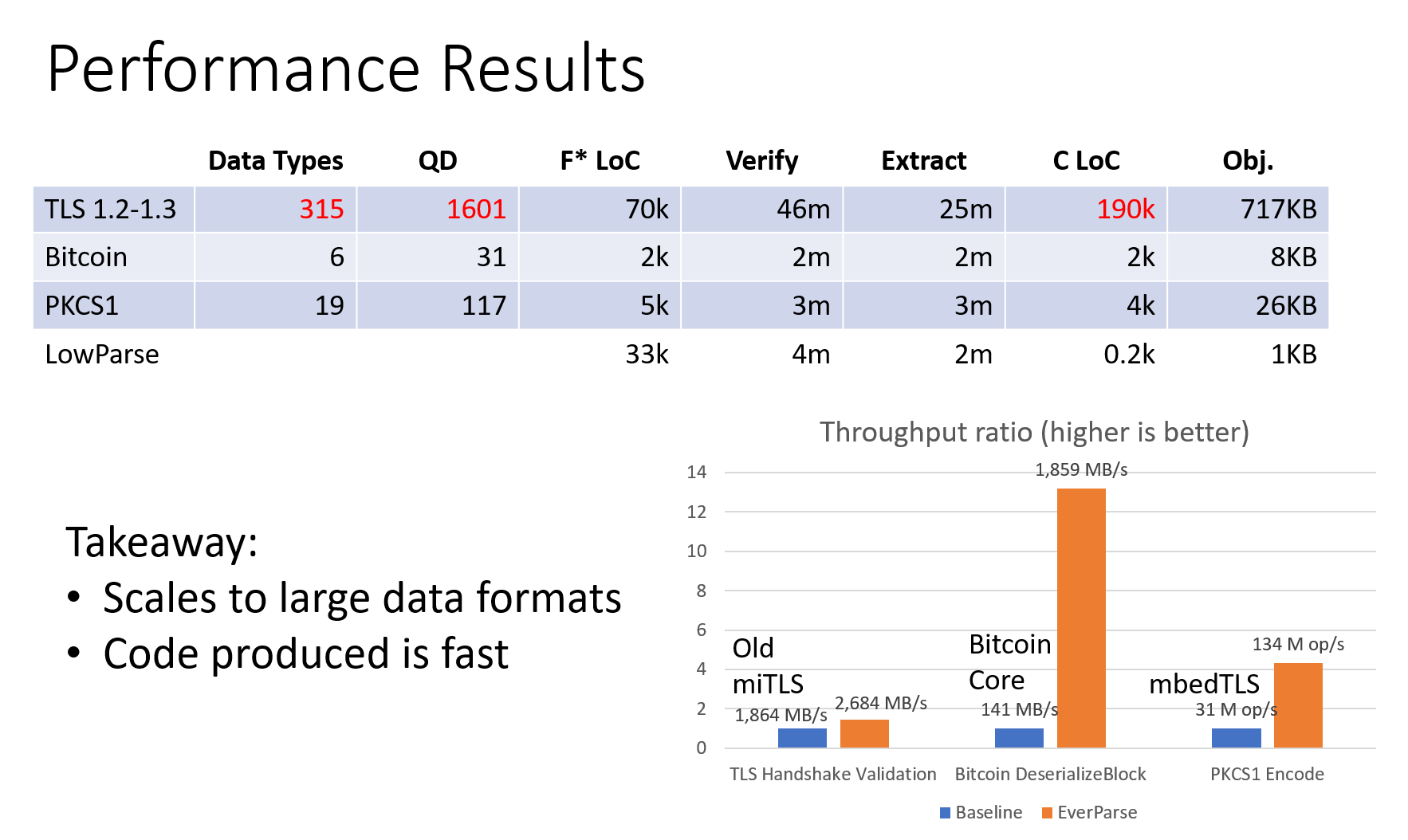
}Performance of extracted C code
Wrapping up
-
Write low-level code if you must
-
But, program it tastefully in a proof assistant, not directly in C or asm
-
Thoughtful structuring of imperative coding patterns can make reasoning about imperative programs similar to functional programming
-
And with proofs, partial evaluation and proof erasure, the resulting code can be significantly faster than hand-written C
-
Homework: Try Chapters 1 – 7 of https://fstar-lang.org/tutorial
Bonus: From F* to SMT
SMT encoding
-
F* verification conditions
- classical, dependently typed, higher-order logic
-
We encode this to SMT
- FOL + equality and function symbols + arithmetic + e-matching
- goals: soundness, predictability, efficiency, scalability
- pragmatic balance between completeness and practical tractability
-
The encoding
- preserves types
- combines a deep and a shallow embedding of F* terms
- allows bounded unrolling of recursive and inductive definitions
- eliminates first-class functions by lambda lifting
- uses SMT-patterns extensively to guide instantiation of quantifiers
- currently targets only Z3 (but some early experiments with CVC4)
Encoding primitive operations and types
-
Primitive types (booleans, integers…) are boxed
(declare-sort Term) (declare-fun BoxInt (Int) Term) (declare-fun BoxInt_proj (Term) Int) (assert (forall ((@x Int)) (= (BoxInt_proj (BoxInt @x)) @x))) (declare-fun Prims.int () Type) (assert (forall ((@x Int)) (HasType (BoxInt @x) Prims.int))))Operators are given shallow semantics:
(assert (forall ((@x Term) (@y Term)) (= (op_Subtraction @x @y) (BoxInt (- (BoxInt_proj @x) (BoxInt_proj @y))))))
Typechecking factorial
type nat = x:int{x>=0}
let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1))- Encoding type
nat:(assert (forall ((@x Term)) (iff (HasType @x nat) (and (HasType @x int) (>= (BoxInt_proj @x) 0))))) - Proving termination:
(declare-fun n () Term) (assert (not (implies (and (HasType n nat) (not (= n (BoxInt 0)))) (Valid (Precedes (op_Subtraction n (BoxInt 1)) n))))) - Can be proved because of this axiom:
(assert (forall ((@x Term) (@y Term)) (implies (and (HasType @x nat) (HasType @y nat) (< (BoxInt_proj @x) (BoxInt_proj @y))) (Valid (Precedes @x @y)))))
Typechecking factorial (2)
type nat = x:int{x>=0}
let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1))- Return value is
nat(declare-fun n () Term) (assert (HasType n nat)) (assert (forall ((@x Term)) (implies (and (HasType @x nat) (Valid (Precedes @x n))) (HasType (factorial @x) nat))))(assert (not (ite (BoxBool_proj (op_Equality int n (BoxInt 0))) (>= 1 0) (>= (BoxInt_proj (op_Multiply n (factorial (op_Subtraction n (BoxInt 1))))) 0 ))))
Allowing SMT solver to do bounded unrolling
type nat = x:int{x>=0}
let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1))(declare-datatypes () ((Fuel (ZFuel) (SFuel (prec Fuel)))))
(declare-fun MaxFuel () Fuel)
(assert (= MaxFuel (SFuel (SFuel ZFuel))))(assert (forall ((@f Fuel) (x Term))
(implies (HasType x nat)
(= (factorial_fuel (SFuel @f) x)
(ite (op_Equality int x (BoxInt 0))
(BoxInt 1)
(op_Multiply x
(factorial_fuel @f
(op_Subtraction x (BoxInt 1)))))))))(assert (forall ((@x Term)) (= (factorial @x) (factorial_fuel MaxFuel @x))))