Proofs of correctness and security for a mixture of C and assembly code

Proofs of Correctness and Security for Programs that Mix C and Assembly

Nik Swamy and Aymeric Fromherz

INRIA Paris

October 9, 2019

Joint work with LOTS of people

Most of them in the room!

Chris, Bryan, Jonathan, Aseem, Tahina, Cedric, Antoine, Christoph, Santiago, Karthik, Benjamin, Marina, Natalia, Jay, …

A disclaimer

“C”: A C-like DSL with a memory model with stacks, heaps, pointers, arrays, malloc, alloca, free
“Assembly”: Subset of X64 assembly with structured control flow, with a low-level memory model (flat array of bytes)
Everything is sequential, no concurrency etc.

Mixing C and Assembly Code

Crypto: Need for speed! Using specialized instruction sets
- AES-GCM: AES-NI on Intel or AMD
- Curve25519: fast mult & delayed carry propagations using Intel ADX

AES-GCM: Authenticated Encryption for 90% of Secure Internet Traffic

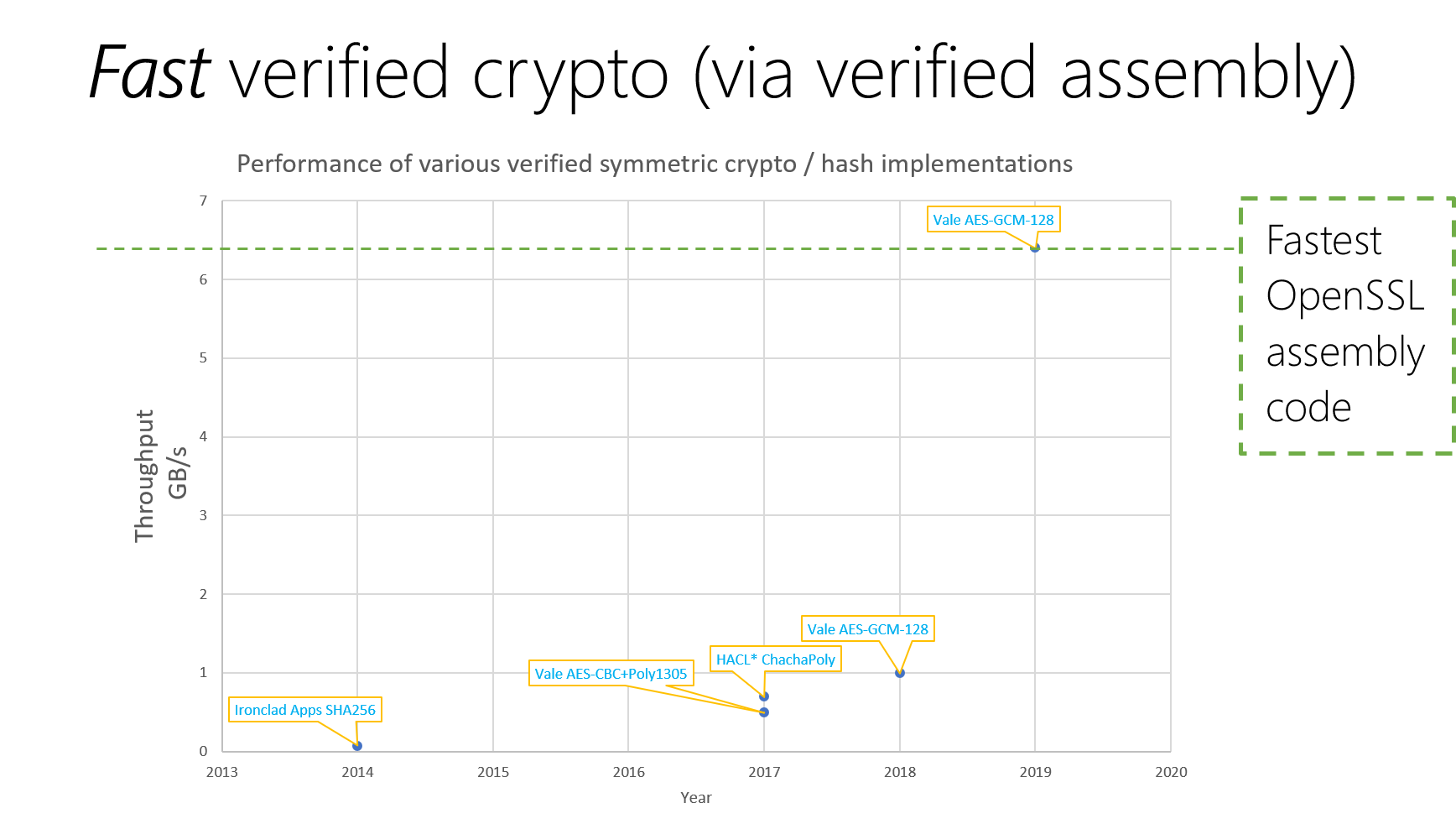
fast-verified-crypto

Mixing C and Assembly Code: Beyond speed

Crypto: Need for speed! Using specialized instruction sets
- AES-GCM: AES-NI on Intel or AMD
- Curve25519: fast mult & delayed carry propagations using Intel ADX
Security
- Closeness to hardware to reason about side-channels
- Could be closer-still! (reflecting micro-architectural details?)
Low-level control
- OS kernel, boot loader, memory allocators, …

Mixing C and Assembly: It's hard to get right!

Can we verify C and assembly together against a single shared spec?
While supporting abstractions suitable for each language
For C:
- A relatively abstract memory model
  - E.g., Allocating typed arrays and structs at abstract addresses
- An abstract calling convention, with named parameters rather than stack slots or registers, platform independent
- Complex types rather than just bytes; i.e., integer types, arrays, structs, …
For assembly:
- A low-level memory model (flat array of bytes)
- Platform-specific calling convention, registers, stack slots etc.
- All operations on bytes or machine words

Rules of the game

Verified C programs call into verified assembly procedures or inline assembly fragments
- Not C in an adversarial assembly context
- Proposing a simple model for verified interoperation. Not verifying compilers, assemblers, linkers
Control transfers from assembly back to C only via returns
- No callbacks from assembly to C
The only observable effects of assembly in C are:
- Updates to memory, observed atomically as assembly returns
- The value in the rax register in the final machine state of the assembly program as it returns to C
- digital side-channels due to the trace of instructions or memory addresses accessed in assembly

Verified C and assembly programs?

Low*: A shallow embedding of C-like DSL in F*
- Verified in a Hoare logic for stateful programs:
```
   let x = malloc 17 in x := 42; free x : ST unit pre post
```
- Verified programs are extracted from F* to C by KreMLin and compiled by gcc, visual c++, compcert, …
Vale: A deep embedding of an X64 assembly subset in F*
- Syntax of assembly programs as a datatype verified in a Hoare logic
```
procedure proc()
requires
    rsi + 8 <= rdi;
ensures
    ...
modifies
    rcx;
{
    Mov(rcx, rdi);
    Add(rcx, rsi); ...}
```
- Verified programs are easily printed in some concrete syntax for assembly

The rest of this talk

MiniLow*: A simplified overview of Low*'s embedding in F* as an effect
MiniVale: A simplified overview of Vale language and its deep embedding in F*
Modeling interop between MiniLow* and MiniVale
Additional challenges generalizing to Vale and Low*
- Inline assembly
- Side channels

Low: A shallow embedding of C in F

Inherit the control constructs, modular structure and typing discipline, partial evaluation capabilities of F*
Verified programs are extracted as usual by F* to an ML-like language
- Very similar to Coq's extraction to OCaml
- Heavy use of erasure and partial evaluation
If the extracted program is first order, doesn't use unbounded inductive types (e.g., no list, tree etc.), … KreMLin emits the program to C after
- translating F* types modeling C constructs to C primitives (e.g, FStar.UInt64.t to uint64_t; array t to t*)
- monomorphizing
- compilation of pattern matches
- bundling fragments into compilation units
- …

The core of Low*

An abstract effect in F* for stateful programming in the C memory model

Abstract monadic effects in F*

A classic state monad:

type st a = s -> (a * s)
let return x h = x,h
let bind f g h = let x,h' = f h in g x h'
let get () h = h,h
let put h _ = (),h

Turned into an abstract “computation type” and can be primitively implemented under the hood or not
```
new_effect ST { st; return; bind; get; put } (* actually, a bit more verbose than that! *)
```
Can now program effectful computations directly:
```
let double () = put (get () + get ())
```
And F* can check double : unit -> ST unit pre post

Hoare triple computation-types

ST a (requires (pre: s -> prop)) (ensures (post: s -> a -> s -> prop))

stateful pre-condition is predicate on initial states
post-condition is relation on initial states, results, and final states

val get ()
  : ST s
    (requires fun s -> True)
    (ensures fun s0 result s1 -> s0 == result /\ result == s1)
    
val put s
  : ST unit
    (requires fun _ -> True)
    (ensures fun _ _ s1 -> s1 == s)

Richer memory models

Program libraries to model memory with pointers to mutable arrays
Derive effectful actions for primitive operations (e.g., !, := etc.)
Write and verify effectful programs against these libraries
Extract them to programs in C with primitive effects

F*:

let incr (p:pointer int) : ST unit 
         (requires fun h0 -> h0 `contains` p)
         (ensures fun h0 _ h1 -> modifies {p} h0 h1 /\ h1.[p] = h0.[p] + 1)
    = p := !p + 1

void incr (int *p) { *p = *p + 1; }

A memory model with mutable arrays

module Memory
  let addr = nat
  (* A memory of mutable arrays: Stores a sequence of values at each address *)
  abstract let mem = {
    next_addr: addr;
    map: addr -> option (a:Type & seq a) {
       forall a. h >= next_addr ==> map a == None
    }
  }

abstract let array t = {
  addr:nat;
  len:nat
}
let ptr t = a:array t{a.len = 1}
let contains m (a:array t) : prop = ...
let sel m (a:array t{m `contains` a}) : seq a = ...
let upd m (a:array t{m `contains` a}) s : mem =  ...

Deriving C-like Effectful Operations

Array indexing: a.[i] extracted to *(a + i)

let ( .[] ) #t (a:array t) (i:nat)
: ST t
  (requires fun h -> h `contains` r /\ i < a.len)
  (ensures fun h0 x h1 -> h0 == h1 /\ x == Seq.index (sel h1 r) i)
= index (sel (get()) a) i

Array update: a.[i] <- v extracted to *(a + i) = v

let ( .[]<- ) #t (a:array t) (i:nat) (v:t)
: ST unit
  (requires fun h -> h `contains` a /\ i < a.len)
  (ensures fun h0 x h1 -> h1 == upd h0 a (Seq.update (sel h0 a) i v))
= let h0 = get () in
  put (upd h0 a (Seq.update (sel h0 a) i v))

Allocating and Freeing references

let malloc #t (i:nat) (x:t)
  : ST (array t)
    (requires fun h -> True)
    (ensures fun h0 a h1 -> modifies {} h0 h1 /\ fresh a h0 h1 /\ sel h1 a == Seq.create i x)
  = ...

let free #t (a:array t)
  : ST unit
    (requires fun h -> h `contains` r)
    (ensures fun h0 () h1 -> modifies {a} h0 h1)
  = ...

That's pretty much it

Well, more libraries modeling

stack allocation
machine integers
strings
various looping constructs
libraries for framing (modifies etc.)
monotonic state

Using this build more libraries, e.g, structured access into validated binary data, specified by parsers and lenses (i.e, EverParse)

Program in Low*; Partially Evaluate; Extract to C

let accessor (p1:parser t1) (p2:parser t2) (l:lens t1 t2) =
    bs:array uint8 ->
    pos:u32 { pos <= length bs } ->
    ST u32 (requires  ...) (ensures ...)

After partial evaluation and proof erasure …

uint32_t Parsers_ClientHello_clientHello_validator(LowParse_Low_Base_slice input, uint32_t pos)
{
uint32_t pos10 = Parsers_ProtocolVersion_protocolVersion_validator(input, pos);
uint32_t pos11;
if (pos10 > ERROR_CODE)
  pos11 = pos10;
else
  pos11 = Parsers_Random_random_validator(input, pos10);
uint32_t pos12;
if (pos11 > ERROR_CODE)
  pos12 = pos11; ...

Vale

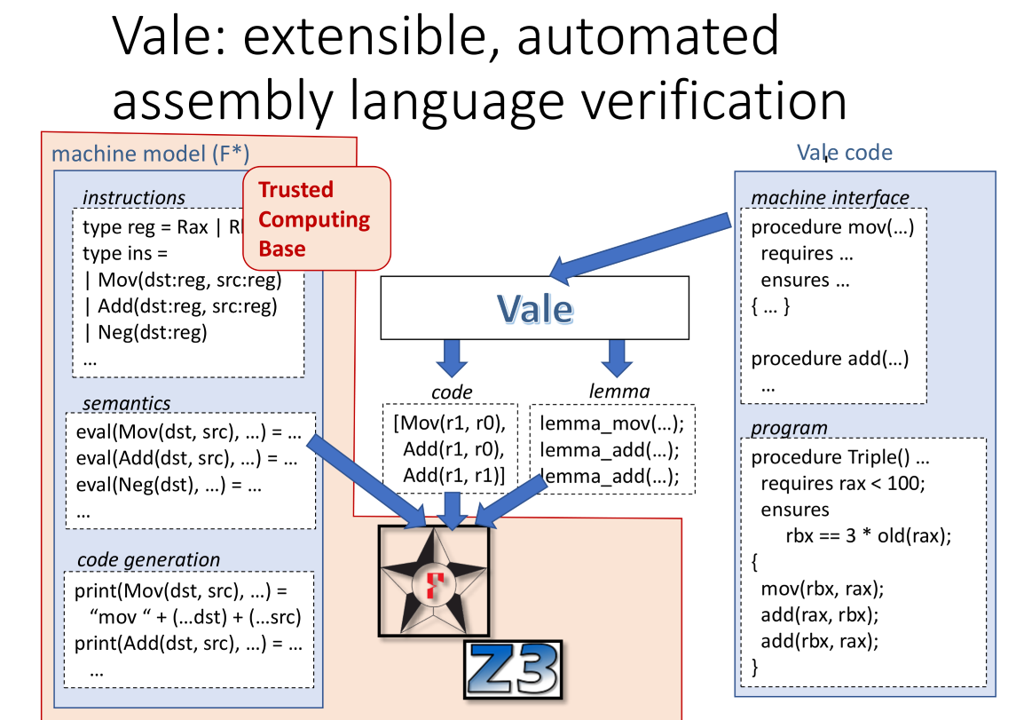
ValeArch

Vale machine model

Registers

type reg = | Rax | Rbx | ... 
let regs_t = Map.t reg nat64

Heap

let heap_t = Map.t nat64 nat8

Machine state

type state_t = {
  regs: regs_t;
  heap: heap_t;
  flags: flags_t;
  stack: stack_t;
  ...
}

Vale instruction set

Very simple and static here, but the real thing is larger and extensible

type operand =
  | Reg of reg
  | Const of nat64
  | Mem of nat64
    
type ins =
  | Mov64: dst:operand -> src:operand -> ins
  | Add64: dst:operand -> src:operand -> ins

type prog =
  | Ins : ins -> prog
  | Block : list prog -> prog
  | WhileLessThan :  src1:operand -> src2:operand -> whileBody:code -> code

Vale semantics

Big-step operational / denotational semantics using an interpreter

val eval (p:prog) (f:fuel) (s:state_t) : option state_t

Deriving a Hoare-style proof rules:

let pre_t = state_t -> prop
let post_t = state_t -> state_t -> prop
(* {pre} c {post}: Also computes the fuel needed to run c *)
let triple (pre:pre_t) (c:prog) (post:post_t) =
    s0:state_t { pre s0 } ->
    (s1:state & f:fuel {
        eval s0 c f == Some s1 /\
        post s0 s1
     })

`memcpy64` : A simple vale program and proof

procedure memcpy64()
    requires/ensures
        (rsi + 64 <= rdi) \/ (rdi + 64 <= rsi); //source and destination arrays are disjoint
        forall(i) rsi <= i < rsi + 64 ==> Map.contains(mem, i);
        forall(i) rdi <= i < rdi + 64 ==> Map.contains(mem, i);
    ensures
        forall(i) 0 <= i && i < 64 ==> mem[rdi + i] == mem[rsi + i];
    reads
        rsi; rdi;
    modifies
        rax; rbx; rcx; rdx; rbp;
        mem;
{
    Load64(rax, rsi, 0);    Load64(rbx, rsi, 8);
    Load64(rcx, rsi, 16);   Load64(rdx, rsi, 24);
    Load64(rbp, rsi, 32);   Store64(rdi, rax, 0);
    Store64(rdi, rbx, 8);   Store64(rdi, rcx, 16);
    Store64(rdi, rdx, 24);  Store64(rdi, rbp, 32);
    Load64(rax, rsi, 40);   Load64(rbx, rsi, 48);
    Load64(rcx, rsi, 56);   Store64(rdi, rax, 40);
    Store64(rdi, rbx, 48);  Store64(rdi, rcx, 56);
}

`memcpy64` : Embedded In F*

let memcpy64_pre : pre_t = fun s ->  r.regs.[Rsi] + 64 <= r.regs.[Rdi] /\ ... 
let memcpy64_code : prog = [ ... instructions ... ]
let memcpy64_post : post_t = fun s0 s1 -> ...
(* Main statement of correctness *)
val memcpy64_correct : triple memcpy64_pre memcpy64_code memcpy64_post

Calling `memcpy64` from Low*

Would like to be able to give it the following spec:

val memcpy64 (dst src:array u8)
   : ST _
    (requires fun m0 ->
        m0 `contains` dst /\
        m0 `contains` src /\
        disjoint dst src /\
        dst.length >= 64 /\
        src.length >= 64)
    (ensures fun m0 _ m1 ->
        modifies { dst } m0 m1 /\
        (forall (i:nat{i<64}). Seq.index (sel m1 dst) i == Seq.index (sel m0 src) i))

But, on what grounds?

Reflect the Vale interpreter as a Low* computation (several steps)

`memcpy64`

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)

`memcpy64`

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)
    let s0 = create_initial_vale_state m0 dst src in (* Build a Vale machine state *)

`memcpy64`

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)
    let s0 = create_initial_vale_state m0 dst src in (* Build a Vale machine state *)
    let s1, f = memcpy64_correct s0 in (* Use the Vale correctness proof to compute the final Vale state *)

`memcpy64`

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)
    let s0 = create_initial_vale_state m0 dst src in (* Build a Vale machine state *)
    let s1, f = memcpy64_correct s0 in (* Use the Vale correctness proof to compute the final Vale state *)
    assert (Some s1 = eval memcpy64_code s0 f); //s1 is really what the interpreter computes

`memcpy64`

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)
    let s0 = create_initial_vale_state m0 dst src in (* Build a Vale machine state *)
    let s1, f = memcpy64_correct s0 in (* Use the Vale correctness proof to compute the final Vale state *)
    assert (Some s1 = eval memcpy64_code s0 f); //s1 is really what the interpreter computes
    ST.put (create_final_lowstar_memory m0 s1 dst src) in (* Read back the final Low* memory *)

`memcpy64`

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)
    let s0 = create_initial_vale_state m0 dst src in (* Build a Vale machine state *)
    let s1, f = memcpy64_correct s0 in (* Use the Vale correctness proof to compute the final Vale state *)
    assert (Some s1 = eval memcpy64_code s0 f); //s1 is really what the interpreter computes
    ST.put (create_final_lowstar_memory m0 s1 dst src) in (* Read back the final Low* memory *)
    U64.from_nat64 (s1.regs.[Rax]) (* Return the value of Rax *)

Reflect the Vale interpreter as a Low* computation

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)
    let s0 = create_initial_vale_state m0 dst src in (* Build a Vale machine state *)
    let s1, f = memcpy64_correct s0 in (* Use the Vale correctness proof to compute the final Vale state *)
    assert (Some s1 = eval memcpy64_code s0 f); //s1 is really what the interpreter computes
    ST.put (create_final_lowstar_memory m0 s1 dst src) in (* Read back the final Low* memory *)
    U64.from_nat64 (s1.regs.[Rax]) (* Return the value of Rax *)

This defines our interop model
- Ensures that specifications from Vale and Low* match up
But
1. How to define create_initial_vale_state and create_final_lowstar_memory?
2. How to do this generically so that we have an interop model once and for all, rather than just an interop model for memcpy?
  - Proving the correctness of this model once and for all

Mapping addresses

We need to map Low* arrays to concrete Vale address ranges
- We don't model memory exhaustion in Low*
- Low* address space is infinite; Vale's is finite
- Need an assumption

Assume the existence of a function that given a (small) list of disjoint Low* arrays, computes concrete Vale addresses for them

let arrays = l:list (array u8) { //at most 2^16 disjoint or equal arrays
  length l < 2^16 /\
  forall a1 a2. a1 `mem` l /\ a2 `mem` l ==>
                a1 == a2 \/ a1 `disjoint` a2
}

assume
val addrs (ars:arrays) : m:(a:array u8 { a in ars } -> nat64 {
//the whole array is mapped to a valid sequence of concrete addresses 
 (forall a in ars. valid_range (m a, m a + a.length)) /\ 
//disjoint arrays are mapped to disjoint concrete addresses
(forall (a1 in ars) (a2 in ars).  a1 `disjoint` a2 ==>
  disjoint_ranges (m a1, m a1 + a1.length) (m a2, m a2 + a2.length))
}

Partially mapping memories

Given an addrs ars one can implement a bidirectional map down and up between Low* Memory.mem to a Vale heap_t, with the following signature capturing:
1. Vale programs can only access addresses that correspond to the live Low* arrays passed to it
2. All live arrays in Low* mem are accurately layed out in Vale memory (i.e., arrays are contiguous)

val down (ars:arrays) (m:mem) : h:heap_t 
val up (ars:arrays) (m0:mem) (h:heap_t{domain h == domain (down ars m0)}) : mem

In reality, also accounts for layout of structured types, e.g., machine integers with endianness

Modeling the calling convention

Model platform-specific calling convention to populate register file

let max_args = if IA.win then 4 else 6
let register_of_arg_i (i:nat{i < max_args}) :  reg =
  if IA.win then //windows calling convention
    match i with
    | 0 -> Rcx | 1 -> Rdx | 2 -> R8 | 3 -> R9
  else
    match i with
    | 0 -> Rdi | 1 -> Rsi | 2 -> Rdx | 3 -> Rcx | 4 -> R8 | 5 -> R9

Populate the initial register file

  let registers_of_args (args:list nat64{length args < max_args}) regs = 
      List.fold_left 
          (fun (regs, i) a -> Regs.upd regs (register_of_arg_i i) a, i + 1)
          (regs, 0)
          args

In reality, also account for spilling arguments on the stack etc.

Relating Vale and Low* states

Assuming an uninterpreted register file indexed by Low* memory:

val init_regs (m:mem) : regs_t

Build the initial vale state

let create_initial_vale_state (m0:mem) (dst src:array u8) =
    let ars = [dst;src] in
    let vale_addrs = List.map (addrs ars) ars in
    let regs = registers_of_args vale_addrs (init_regs m0) in
    let h0 = down ars m0 in
   {    regs = regs;
        heap = h0;
        stack = ...;
        flags = ...; }

The final Low* state:

let create_final_lowstar_memory m0 s1 dst src = up [dst;src] m0 s1.heap

Doing it generically

memcpy64: What here is specific to memcpy64?

let memcpy64 dst src =
    let m0 = ST.get () in (* Get the initial Low* memory *)
    let s0 = create_initial_vale_state m0 dst src in (* Build a Vale machine state *)
    let s1, f = memcpy64_correct s0 in (* Use the Vale correctness proof to compute the final Vale state *)
    ST.put (create_final_lowstar_memory m0 s1 dst src) in (* Read back the final Low* memory *)
    s1.regs.[Rax] (* Return the value of Rax *)

Arity (and types) of arguments dst:array u8, src:array u8
The correctness lemma to call
But, we have dependent types! We should be able to generalize this with a bit of generic programming

An arity-generic signature of a Vale wrapper

A simply-typed n-ary arrow

let rec n_arrow (n:nat{ n < max_args }) (result:Type) = 
    if n = 0 then result
    else nat64 -> n_arrow (n - 1) result

Type of a generic Vale wrapper

let rec wrapper_t (n:arity) 
                  (pre:n_arrow n pre_t) 
                  (post:n_arrow n post_t)
                  (args:arrays) =
if n = 0 then 
  unit -> ST U64.t
  (requires fun m0 ->
      pre (create_vale_state args m0))
  (ensures fun m0 v m1 ->
      post (create_vale_state args m0)
             { create_vale_state args m1 with Regs.rax = U64.as_nat v} )
else 
  a:array u8 -> wrapper_t (n - 1) (pre a) (post a) (args @ [ a ])

An arity-generic Vale wrapper

let rec call_assembly (n:arity) (c:code) (pre:n_arrow n pre_t) (post:n_arrow n post_t)
                      (correctness:n_triple pre c post)
                      (args:arrays)
    : wrapper_t n pre post args
    = if n = 0 then
        fun () -> 
            let m0 = ST.get () in
            let s0 = create_initial_vale_state m0 args in
            let s1, f = correctness s0 in
            ST.put (create_final_lowstar_memory m0 s1 args) in
            U64.from_nat (s1.regs.[Rax])
      else 
          fun (x:array u8) -> 
              call_assembly (n - 1) c (pre x) (post x) (correctness x) (args @ [x])

let memcpy64 dst src =
  call_assembly 2 memcpy64_code memcpy64_pre memcpy64_post memcpy64_correct [dst;src]

Phew … but there's still lots left out

Not just array u8: u8, ..., u128, with endianness etc., and arrays of them, mutability qualifiers, disjointness, taint, …
Enforcing that Vale functions always respect their side of the calling convention, leaving stacks in the right shape etc.
Multiple layers of untrusted semantics so that proofs of Low* code calling assembly do not have to reason about low-level abstraction like create_initial_vale_state
Inline assembly and custom calling conventions
Relating side-channel guarantees

Application: Curve25519

Highly optimised bignum modular arithmetic with Intel ADX: fadd, fsub
Glueing pieces together in C

void point_double(uint64_t* nq) {
  ...
  fadd(...);
  fsub(...);
  fsqr2(...);
  ... }

Inline assembly

Custom calling conventions
Custom clobbered registers

static inline void fadd(uint64_t* arg0, uint64_t* arg1, uint64_t* arg2) {
  //custom register mapping
  register uint64_t* arg0_r asm("rdi") = arg0; 
  register uint64_t* arg1_r asm("rsi") = arg1;
  register uint64_t* arg2_r asm("rdx") = arg2;
  
  __asm__ __volatile__(
    "  movq 0(%%rdx), %%r8;"
    "  addq 0(%%rsi), %%r8;"
    ...
  : "+&r" (arg2_r)    //outputs
  : "r" (arg0_r), "r" (arg1_r) //inputs
  : "%rax", "%rcx", "%r8", … //clobbered
}

Modeling custom calling conventions

Previously

let s0 = create_initial_vale_state m0 [arg0;arg1;arg2] in

Now

let s0 = create_initial_vale_state m0 [arg0;arg1;arg2]
                                   (args_regs:i:nat{i < arity} -> reg) in

Restrictions
- Cannot use rsp for arguments
- Different arguments in different registers

Modeling custom clobbered registers

Previously
```
  let s1, f = fadd_correct s0 in
```

Now

  let s1, f = fadd_correct s0 in
  assert (only_modified modified_regs s0 s1);

Printing inline assembly

Reuse most of the Vale assembly printer to extract inline assembly

register uint64_t* arg0_r asm({args_regs 0}) = arg0;

__asm__ __volatile__(
  { vale_printer(code) }
:
: "r" (arg0_r)
: {modified_regs}, "%memory", "%cc"
}

Vale side-channel robustness

Certified taint analysis checking secret-independence of implementations
Correctness of the analysis proven on the deeply embedded Vale semantics, instrumented with observation traces

//noninterference property
let isConstantTime (s1 s2:state) (code:code) (f:fuel) public_vals =
  let r1 = eval code s1 f in
  let r2 = eval code s2 f in
  public_vals(s1) == public_vals(s2) /\ s1.trace == s2.trace ==>
           public_vals(r1) == public_vals(r2) /\ r1.trace == r2.trace

//partially decides isConstantTime
val taint_analysis (code:code) public_vals 
  : b:bool{b ==> forall s1 s2 f. isConstantTime s1 s2 code f public_vals}

Low* side-channel robustness

Secret-independence through type abstraction: type sec64
Only constant-time operations for secret integers:

val add: sec64 -> sec64 -> sec64
Cannot use secret integers to branch or access memory
Metatheorem (on paper) ensuring that execution traces of such programs do not depend on secret values

Relating Vale and Low* side-channel guarantees

Vale programs can be seen as atomic Low* computations
Success of the Vale taint analysis ensures secret independent Vale execution traces
Extended metatheorem: Low* traces now include Vale traces; prove that extended Low* traces are secret independent
At extraction time, run the Vale taint analysis with secrets labels from Low* types

Vale and Low*, in practice

31 Low* calls into Vale assembly
CPU features detection, parts of cryptographic algorithms, full cryptographic implementations
Our biggest call: AES-GCM. 17 arguments, 200 lines of specification

Conclusions and Future Work

Multi-language/multi-abstraction programs are unavoidable in real systems
With our multi-language embedding, prove joint theorems to ensure that specifications don't drift and providing an end-to-end guarantee
- Aiming for simplicity of the model targeting interop of verified programs
Future directions:
- Connect to CompCert?
- Useful for reasoning about secure subsystems? Enclave SDKs?
- Any connections to secure compilation?
And, oh, generic programming is awesome

Proofs of Correctness and Security for Programs that Mix C and Assembly

Joint work with LOTS of people

A disclaimer

Mixing C and Assembly Code

AES-GCM: Authenticated Encryption for 90% of Secure Internet Traffic

Mixing C and Assembly Code: Beyond speed

Mixing C and Assembly: It's hard to get right!

Rules of the game

Verified C and assembly programs?

The rest of this talk

Low*: A shallow embedding of C in F*

The core of Low*

Abstract monadic effects in F*

Hoare triple computation-types

Richer memory models

A memory model with mutable arrays

Deriving C-like Effectful Operations

Allocating and Freeing references

That's pretty much it

Program in Low*; Partially Evaluate; Extract to C

Vale

Vale machine model

Vale instruction set

Vale semantics

memcpy64 : A simple vale program and proof

memcpy64 : Embedded In F*

Calling memcpy64 from Low*

Reflect the Vale interpreter as a Low* computation (several steps)

memcpy64

memcpy64

memcpy64

memcpy64

memcpy64

memcpy64

Reflect the Vale interpreter as a Low* computation

Mapping addresses

Partially mapping memories

Modeling the calling convention

Relating Vale and Low* states

Doing it generically

An arity-generic signature of a Vale wrapper

An arity-generic Vale wrapper

Phew … but there's still lots left out

Application: Curve25519

Inline assembly

Modeling custom calling conventions

Modeling custom clobbered registers

Printing inline assembly

Vale side-channel robustness

Low* side-channel robustness

Relating Vale and Low* side-channel guarantees

Vale and Low*, in practice

Conclusions and Future Work

Low: A shallow embedding of C in F

`memcpy64` : A simple vale program and proof

`memcpy64` : Embedded In F*

Calling `memcpy64` from Low*

`memcpy64`

`memcpy64`

`memcpy64`

`memcpy64`

`memcpy64`

`memcpy64`