Programming and Verifying Effectful Programs in F*
The divergence effect (Dv)
- Some useful code really is not always terminating
val eval : exp -> Dv exp let rec eval e = match e with | App (Lam x e1) e2 -> eval (subst x e2 e1) | App e1 e2 -> eval (App (eval e1) e2) | Lam x e1 -> Lam x (eval e1) | _ -> e let main = eval (App (Lam 0 (App (Var 0) (Var 0))) (Lam 0 (App (Var 0) (Var 0))))./Divergence.exe
F* effect system encapsulates effectful code
-
Pure code cannot call potentially divergent code
-
Only pure code can appear in specifications
val eval : expr -> Dv exprtype tau = e:expr{e = eval e'} ^^^^^^ Expected a pure expression; got an expression ... with effect "DIV" -
Sub-effecting:
Tot t <: Dv t
(e.g. divergent code can include pure code)val subst : list (var * expr) -> expr -> Tot expr eval (subst [x, Num 0] e) : Dv expr
Verifying potentially divergent programs
(partial correctness)
- Using refinement types
val factorial : int -> Dv int - Or the
Divcomputation type (pre- and post- conditions)val eval_closed : e:exp{closed e} -> Dv (e':exp{Lam? e' /\ closed e'}) let rec eval_closed e = match e with | App e1 e2 -> let Lam e1' = eval_closed e1 in below_subst_beta 0 e1' e2; eval_closed (subst (sub_beta e2) e1') | Lam e1 -> Lam e1
Monadic effects in F*
- A classic state monad:
type st a = s -> (a * s)
let return x h = x,h
let bind f g h = let x,h' = f h in g x h'
let get () h = h,h
let put h _ = (),h-
Turned into an abstract “computation type” and can be primitively implemented under the hood or not
new_effect STATE { st; return; bind; get; put } -
Can now program effectful computations directly:
let double () = put (get () + get ()) -
And F* infers
double : unit -> STATE unit w
Specifying Effectful Programs
-
Type inference in F* includes inference of weakest preconditions
-
e : STATE a wmeansforall post h0. //for all postconditions and initial states w post h0 ==> //given the weakest precondition is valid for post and h0 e h0 ~>* (v, h1) /\ //the computation reduces to a value and final state post (v, h1) //that validate the postcondition -
What is a weakest precondition predicate transformer?
let st_wp a : st_post a -> st_pre //transforms postconditions to preconditions where st_post a : (a * s) -> prop //postconditions relate results to memories and st_pre : s -> prop //preconditions are memory predicates -
Dijkstra monad for state
WP inference CPS tranform
let st_wp a : st_post a -> st_pre //transforms postconditions to preconditions
where st_post a : (a * s) -> prop //postconditions relate results to memories
and st_pre : s -> prop //preconditions are memory predicates- Hey, wait a minute … isn't that like the continuation monad?
cont r a = (a -> r) -> r-
Take the continuation monad with result type
props -> cont prop (a * s) = s -> ((a * s) -> prop) -> prop ~ ((a * s) -> prop) -> s -> prop = st_post a -> st_pre = st_wp a -
WPs for state are just the state monad transformer applied to the continuation monad with result type
propstateT m a = s -> m (a * s) st_wp a = stateT (cont prop) a
Auto-generating WP calculi for monads
-
F* automatically derives a weakest precondition calculus for m-effectful computations whose WPs have the form
m_wp a = mT (cont prop) a- the
mtransformer on the continuation monad with result typeprop
- the
-
And infers computations types of the form
M a (wp : m_wp a) -
E.g., for exceptions
ex_wp a = ex_t (cont prop) a = (option a -> prop) -> prop -
For state + exceptions
st_ex_wp a = state_t (ex_t (cont prop)) a = s -> (ex_t (cont prop) a * s) = s -> ((option a * state) -> prop) -> prop ~ ((option a * state) -> prop) -> s -> prop = st_ex_post a -> st_ex_pre
Derived Specifications: Hoare triples
-
Reasoning about continuations: great for a core logic / not for a human
-
Hoare logic-style pre-conditions and post-conditions
ST a (pre: s -> prop) (post: s -> a -> s -> prop) = STATE a (fun k s0 -> pre s0 /\ (forall x s1. post s0 x s1 ==> k (x, s1))) -
stateful pre-condition is predicate on initial states
-
post-condition is relation on initial states, results, and final states
val get ()
: ST s
(requires fun s -> True)
(ensures fun s0 result s1 -> s0 == result /\ result == s1)
val put s
: ST unit
(requires fun _ -> True)
(ensures fun _ _ s1 -> s1 == s0)Richer Model of Mutable Memory
with Lens-indexed Imperative Lenses
Richer memory models
-
Program libraries to model memory, e.g., the ML heap
-
Derive effectful actions for primitive operations (e.g.,
!,:=etc.) -
Write effectful programs against these libraries and verify them with refined computation types
-
Extract them to programs in ML or C with primtive effects
-
F*:
let incr (r:ref int) : ST unit (requires (fun _ -> True)) (ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\ sel h2 r = sel h1 r + 1)) = r := !r + 1ML:
let incr (r:ref int) : unit = r := !r + 1C:
void incr (int *r) { *r = *r + 1; }
Modeling the ML heap
A sketch of FStar.Heap:
module Heap
let addr = nat
abstract let heap = {
next_addr: addr;
map: addr -> option (a:Type & v:a) {
forall a. h > next_addr ==> map a == None
}
}
abstract let ref t = addr
let contains h (r:ref t) = r < h.next_addr /\ h.map r == Some (t, _)
let sel h (r:ref t{h `contains` r}) = let Some (_, v) = h.map r in v
let upd h (r:ref t{h `contains` r}) v = ...
Deriving ML-like Effectful Operations
-
Reading references
let (!) #t (r:ref t) : ST t (requires fun h -> h `contains` r) (ensures fun h0 x h1 -> h0 == h1 /\ x = sel h1 r) = sel (get()) r -
Writing references
let (:=) #t (r:ref t) (v:t) : ST (ref t) (requires fun h -> h `contains` r) (ensures fun h0 x h1 -> h1 == upd h0 r v) = put (upd (get()) r v); r -
Allocating and freeing references …
Freeing references
let free #r (r:ref t)
: ST unit
(requires fun h -> h `contains` r)
(ensures fun h0 () h1 -> modifies !{r} h0 h1)
= let h = get () in
put ({h with map = fun a -> if a = r then None else h.map a})Reference swapping (hand proof sketch)
val swap : r1:ref int -> r2:ref int -> ST unit
(requires (fun h0 -> True))
(ensures (fun h0 _ h3 -> modifies !{r1,r2} h0 h3 /\
sel h3 r2 == sel h0 r1 /\ sel h3 r1 == sel h0 r2))
let swap r1 r2 =
let t = !r1 in
(* Know (P1): exists h1 t. modifies !{} h0 h1 /\ t == sel h0 r1 *)
r1 := !r2;
(* Know (P2): exists h2. modifies !{r1} h1 h2 /\ sel h2 r1 == sel h1 r2 *)
r2 := t
(* Know (P3): modifies !{r2} h2 h3 /\ sel h3 r2 == t *)(* `modifies !{r1,r2} h0 h3` follows directly from transitivity of modifies *)
(* `sel h3 r2 == sel h0 r1` follows immediately from (P1) and (P3) *)
(* Still to show: `sel h3 r1 == sel h0 r2`
From (P2) we know that `sel h2 r1 == sel h1 r2` (A)
From (P1) we know that modifies !{} h0 h1
which by definition gives us sel h1 r2 == sel h0 r2 (B)
From (P3) we know that modifies !{r2} h2 h3
which by definition gives us sel h2 r1 == sel h3 r1 (C)
We conclude by transitivity from (A)+(B)+(C) *)- This variant is correct even when
r1andr2are aliased
Bidirectional data access, abstractly with lenses
type lens a b = {
get : a -> b;
put : b -> a -> a
}selandupdform a lenslet ref_lens : lens (heap * ref a) a = { get = fun (h, r) -> sel h r; put = fun v (h, r) -> upd h r v }
Imperative lenses
-
A lens-indexed computation type:
type st_lens inv (l:lens (heap * a) b) = { st_get : x:a -> ST b (requires fun h -> inv h x) (ensures fun h0 y h1 -> h0==h1 /\ y == l.get (h0, x)); st_put : y:b -> x:a -> ST a (requires fun h -> inv h x) (ensures fun h0 x' h1 -> h1, x' == l.put y (h0, x)) } -
(!) and (:=) are imperative lenses
let iref_lens : st_lens contains ref_lens = { st_get = (!); st_put = (:=); }
Manipulating Binary-formatted Data
with the EverParse parser combinator library
Networking Protocols: Many performance and security-critical parsers
-
TLS 1.3 message format, with variable-length data
uint16 ProtocolVersion; opaque Random[32]; uint8 CipherSuite[2]; struct { ProtocolVersion legacy_version = 0x0303; Random random; opaque legacy_session_id<0..32>; CipherSuite cipher_suites<2..2^16-2>; opaque legacy_compression_methods<1..2^8-1>; Extension extensions<8..2^16-1>; } ClientHello; -
De facto: Hand-written parsers and formatters, for performance, but also many vulnerabilities
- Heartbleed was a parsing bug
EverParse: A Verified Low-level Parser Generator
-
Given a type description (e.g., ClientHello)
-
Produces a parser and a formatter indexed by its (inverse) parser
let parser t = b:bytes -> option (t * n:nat{n <= length b})
let format (p:parser t) = f:(t -> bytes) {
forall x. p (f x) == Some (x, length (f x))
}- And a low-level zero-copy validator indexed by the parser
let validator (p:parser t) = bs:array uint8 -> pos:u32 { pos <= length bs } -> ST u32 (requires fun h0 -> h0 `contains` bs) (ensures fun h0 res h1 -> h0 == h1 /\ (if res < ERROR_CODE then exists v. p (as_bytes bs h0 pos) = Some (v, res) (* parsing succeeds *) else p (as_bytes bs h0 pos) = None (* parsing fails *)))
Combinator library for validators
- Mirroring the structure of parser combinators
val return : validator unit_parser
val bind : validator p -> (t -> validator q) -> validator (p `Parser.bind` q)
val seq: validator p -> validator s -> validator (p `Parser.seq` s)
val map : f:(t -> s) -> validator p -> -> validator (Parser.map f p)
...-
Client-hello validator
protocolVersion_validator `seq` random_validator `seq` sessionID_validator `seq` clientHello_cipher_suites_validator `seq` clientHello_compression_method_validator `seq` clientHelloExtensions_validator -
Imperative code refines pure parser by construction
Data accessors
- Structured access into validated binary data, specified by parsers and lenses
let accessor (p1:parser t1) (p2:parser t2) (l:lens t1 t2) =
bs:array uint8 ->
pos:u32 { pos <= length bs } ->
ST u32
(requires fun h0 ->
h0 `contains` bs /\
Some? (p1 (as_bytes bs h0 pos))) (* bs contains a valid t1 *))
(ensures fun h0 res h1 ->
h0 == h1 /\
let Some (v1, _) = p1 (as_bytes bs h0 pos) in
p2 (as_bytes bs h0 res) == Some (l.get v1, _)) (* returns offset to t2 *)
-
Abstractly, structured data access into a (representation of)
t1 -
Concretely, just performs arithmetic into the binary formatted data
- Effectively, reads directly from computed offsets into network packets
- Would be crazy to try this directly in C!
Extracted to efficient C code
- After partial evaluation and proof erasure …
uint32_t Parsers_ClientHello_clientHello_validator(LowParse_Low_Base_slice input, uint32_t pos)
{
uint32_t pos10 = Parsers_ProtocolVersion_protocolVersion_validator(input, pos);
uint32_t pos11;
if (pos10 > ERROR_CODE)
pos11 = pos10;
else
pos11 = Parsers_Random_random_validator(input, pos10);
uint32_t pos12;
if (pos11 > ERROR_CODE)
pos12 = pos11;
else
pos12 = Parsers_SessionID_sessionID_validator(input, pos11);
uint32_t pos13;
if (pos12 > ERROR_CODE)
pos13 = pos12;
else
pos13 = Parsers_ClientHello_cipher_suites_clientHello_cipher_suites_validator(input, pos12);
uint32_t pos1;
...
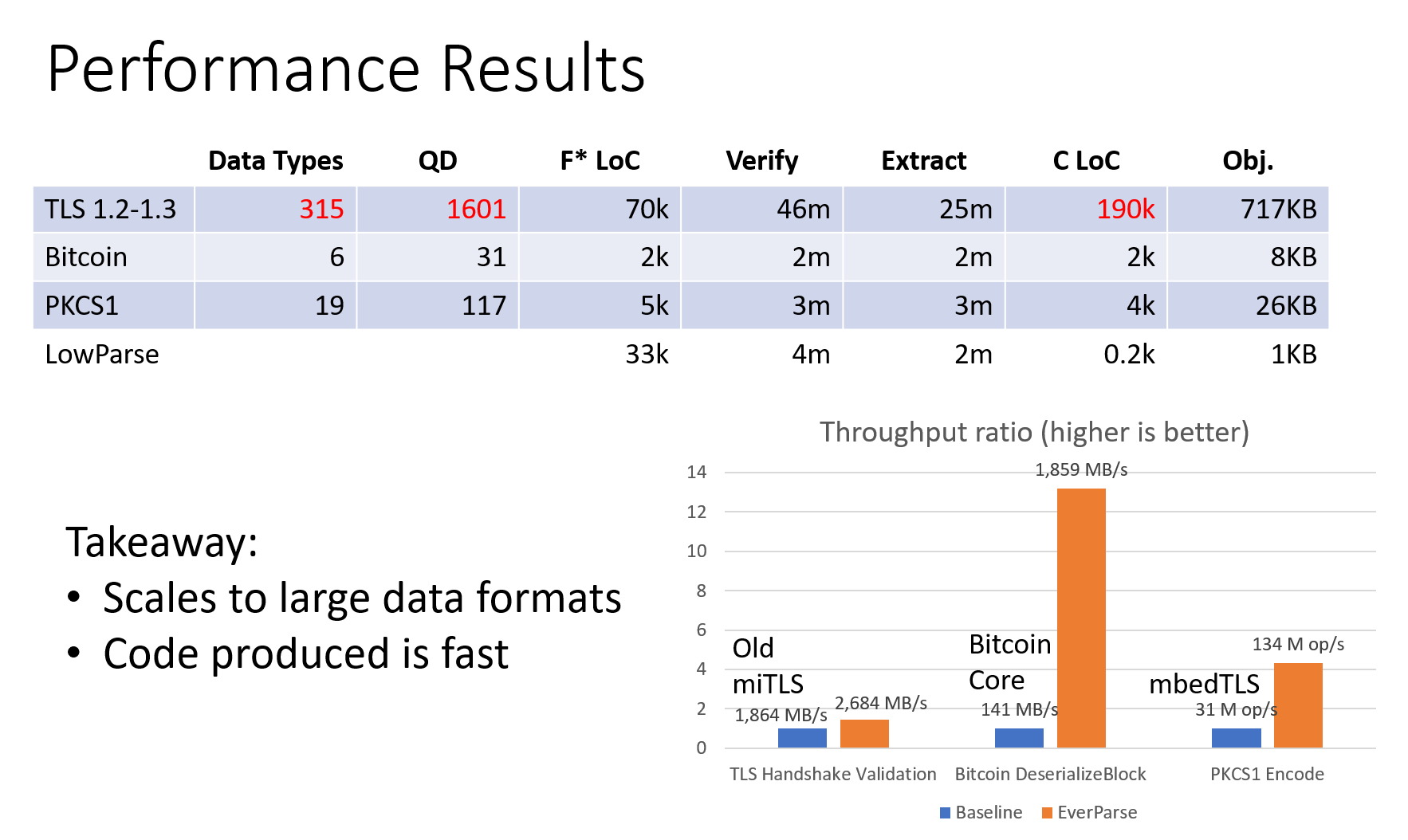
}Performance of extracted C code
Wrapping up
-
Write low-level code if you must
-
But, program it tastefully in a proof assistant, not directly in C or asm
-
Thoughtful structuring of imperative coding patterns can make reasoning about imperative programs similar to functional programming
-
And with proofs, partial evaluation and proof erasure, the resulting code can be significantly faster than hand-written C
-
Homework: Try Chapters 1 – 7 of https://fstar-lang.org/tutorial
