Layering Effectful Languages

Richer Memory Models, Low*, and EverParse

fstar-logo

Nik Swamy

Microsoft Research

Oregon Programming Languages Summer School (OPLSS), 2021

Last time

  • … we saw how to deeply embed language and build certified tools for them

    • Vale and its VC generator

  • … we saw how to shallowly embed effectful languages and reason about them with refined computation types

    • Dijkstra monad for state
    • Also, information flow controls (see the notes)

Richer Model of Mutable Memory

with Lens-indexed Imperative Lenses

Richer memory models

  • Program libraries to model memory, e.g., the ML or C heap

  • Derive effectful actions for primitive operations (e.g., !, := etc.)

  • Write effectful programs against these libraries and verify them with refined computation types

  • Extract them to programs in ML or C with primitive effects

    F*: 

    let incr (r:ref int)
  : ST unit
    (requires fun h0 -> h0 `contains` r)
    (ensures fun h0 _ h1 -> sel h1 r = sel h0 r + 1)
  = r := !r + 1

    ML: 

    let incr (r:ref int) : unit = r := !r + 1

    C: 

    void incr (int *r) { *r = *r + 1; }

Modeling the ML heap

A sketch of FStar.Heap: 

module Heap
  let addr = nat
  abstract let heap = {
    next_addr: addr;
    map: addr -> option (a:Type & v:a) {
       forall a. h > next_addr ==> map a == None
    }
  }
  abstract let ref t = addr  
  let contains h (r:ref t) = r < h.next_addr /\ h.map r == Some (t, _)
  let sel h (r:ref t{h `contains` r}) = let Some (_, v) = h.map r in v
  let upd h (r:ref t{h `contains` r}) v = ...

More on modeling heaps

Deriving ML-like Effectful Operations

  • Reading references 

    let (!) #t (r:ref t)
  : ST t
      (requires fun h -> h `contains` r)
      (ensures fun h0 x h1 -> h0 == h1 /\ x = sel h1 r) =
  sel (get()) r

  • Writing references 

    let (:=) #t (r:ref t) (v:t)
  : ST (ref t)
      (requires fun h -> h `contains` r)
      (ensures fun h0 x h1 -> h1 == upd h0 r v) =
  put (upd (get()) r v); r

  • Allocating and freeing references …

Bidirectional data access, abstractly with lenses

type lens a b = {
    get : a -> b;
    put : b -> a -> a
}
  • sel and upd form a lens 
    let ref_lens : lens (heap * ref a) a  = {
  get = fun (h, r) -> sel h r;
  put = fun v (h, r) -> upd h r v
}

Imperative lenses

  • A lens-indexed computation type: 

    type st_lens inv (l:lens (heap * a) b) = {
 st_get : x:a
       -> ST b
          (requires fun h -> inv h x)
          (ensures fun h0 y h1 -> h0==h1 /\ y == l.get (h0, x));

 st_put : y:b 
       -> x:a 
       -> ST a
          (requires fun h -> inv h x)
          (ensures fun h0 x' h1 -> h1, x' == l.put y (h0, x))
}

  • (!) and (:=) are imperative lenses 

    let iref_lens : st_lens contains ref_lens = {
  st_get = (!);
  st_put = (:=);
}

More on lens-indexed imperative lenses

Low*: A shallow embedding of C in F*

  • Inherit the control constructs, modular structure and typing discipline, partial evaluation capabilities of F*

  • Verified programs are extracted as usual by F* to an ML-like language

    • Very similar to Coq's extraction to OCaml

    • Heavy use of erasure and partial evaluation

  • If the extracted program is first order, doesn't use unbounded inductive types (e.g., no list, tree etc.), … KreMLin emits the program to C after

    • translating F* types modeling C constructs to C primitives (e.g, FStar.UInt64.t to uint64_t; array t to t*)

    • monomorphizing

    • compilation of pattern matches

    • bundling fragments into compilation units

    • …

A Demo of Low*

Applications of Low*

The Essence of Low*

  • HyperStack: A region-based memory model for stacks and heaps

    • Building on a primitive notion of monotonic state

  • Heap reasoning with implicit dynamic frames

  • Libraries with specialized extraction via Kremlin

    • Machine integers
    • Arrays
    • Looping combinators

HyperStack: The Low* Memory Model

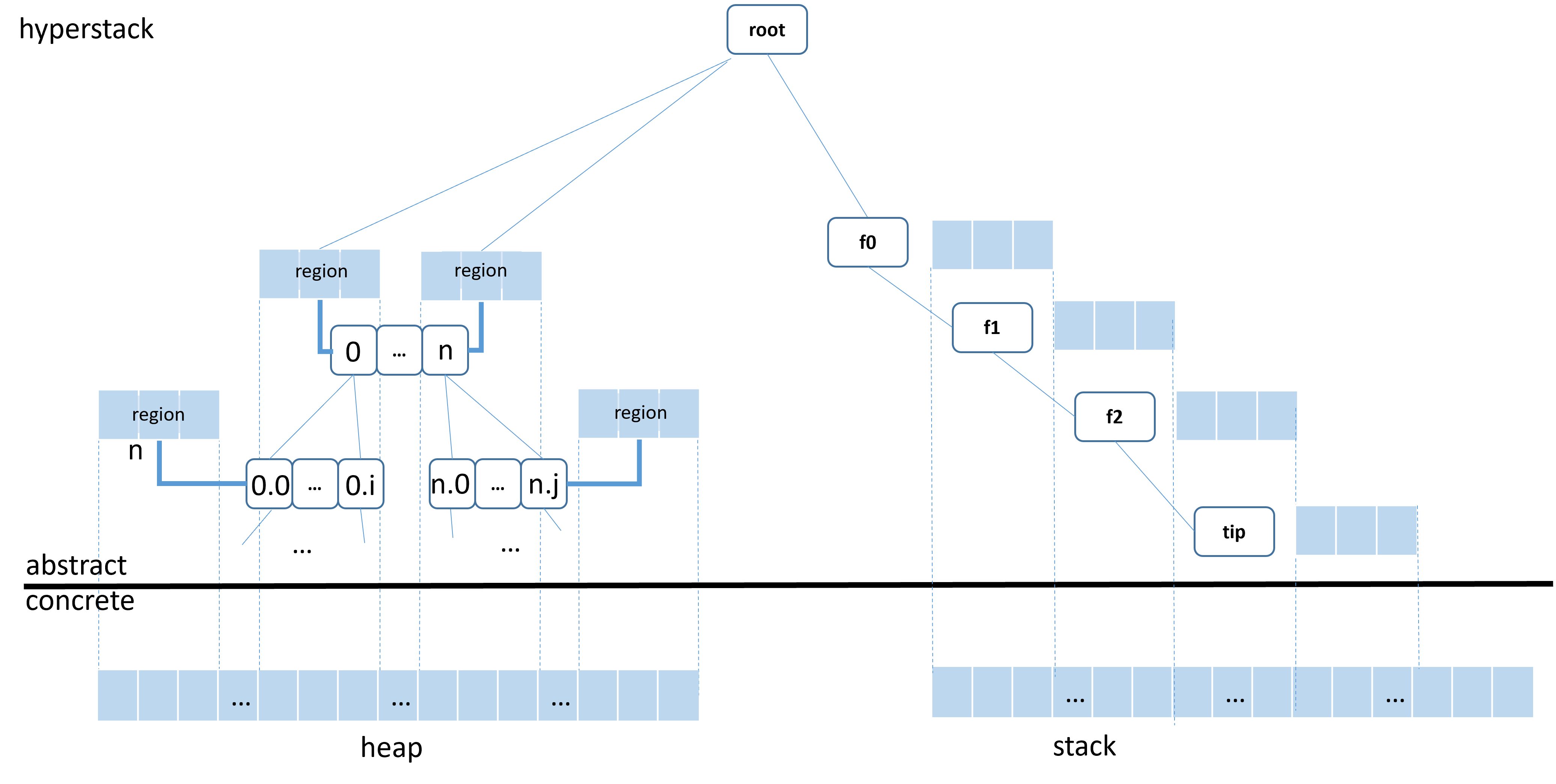
HyperStack

  • A key ingredient in defining this memory model, an effect of monotonic state: Recalling a Witness

Heap Reasoning with Implicit Dynamic Frames

let incr (p:pointer int)
    : ST unit 
      (requires fun h0 -> h0 `contains` p)
      (ensures fun h0 _ h1 -> modifies {p} h0 h1 /\ h1.[p] = h0.[p] + 1)
    = p := !p + 1

  • modifies l h0 h1, where l : loc abstracts an aggregation of memory locations

  • Stateful specifications are heavily reliant on modifies for “framing”

    • Describing only what changed, all other existing locations in the heap remained the same

  • Later, we'll see other ways to handle framing, notably with separation logic

Libraries with primitive support in KReMLin

  abstract let array t = { len:nat ; base:ref (s:seq t {lengths  = len}) }
  let ptr t = a:array t{a.len = 1}
  let contains m (a:array t) : prop = ...
  let sel m (a:array t{m `contains` a}) : seq a = ...
  let upd m (a:array t{m `contains` a}) s : mem =  ...

  • Array indexing: a.[i] extracted to *(a + i) 

    let ( .[] ) #t (a:array t) (i:nat)
: ST t
  (requires fun h -> h `contains` r /\ i < a.len)
  (ensures fun h0 x h1 -> h0 == h1 /\ x == Seq.index (sel h1 r) i)
= index (sel (get()) a) i

  • Array update: a.[i] <- v extracted to *(a + i) = v 

    let ( .[]<- ) #t (a:array t) (i:nat) (v:t)
: ST unit
  (requires fun h -> h `contains` a /\ i < a.len)
  (ensures fun h0 x h1 -> h1 == upd h0 a (Seq.update (sel h0 a) i v))
= let h0 = get () in
  put (upd h0 a (Seq.update (sel h0 a) i v))

Automating Domain-specific Low* Proofs

  • You can program and prove code in Low* directly

    • Lots of instances of that, but proofs are still hard

  • But, you can also metaprogram Low*

    • E.g., HACLxN: Metaprogrammed vectorized cryptography and cryptographic agility

  • Or, build further proof-oriented DSLs on top of Low*

Manipulating Binary-formatted Data with the EverParse Combinator Library

EverParse-OPLSS2021.pptx

Wrapping up

  • Write low-level code if you must

  • But, program it tastefully in a proof assistant, not directly in C or asm

  • Thoughtful structuring of imperative coding patterns can make reasoning about imperative programs similar to functional programming

  • And with proofs, partial evaluation and proof erasure, the resulting code can be significantly faster than hand-written C