Introduction to Programming and Verification in F*
A first taste
-
Write ML-like code
let rec factorial n = if n = 0 then 1 else n * factorial (n - 1) -
Give it a specification, claiming that
factorialis a total function from non-negative to positive integers.val factorial: n:int{n >= 0} -> i:int{i >= 1} -
Ask F* to check it
fstar factorial.fst Verified module: Factorial All verification conditions discharged successfully
fstar factorial.fst
Verified module: Factorial
All verification conditions discharged successfullyF* builds a typing derivation of the form:
-
In a context including definitions of F* primitives
-
The program has type , given the validity of a logical formula
-
is passed to Z3 (an automated theorem prover/SMT solver) to check for validity
-
If the check succeds, then, from the metatheory of F*, the program is safe at type
Running F* Programs
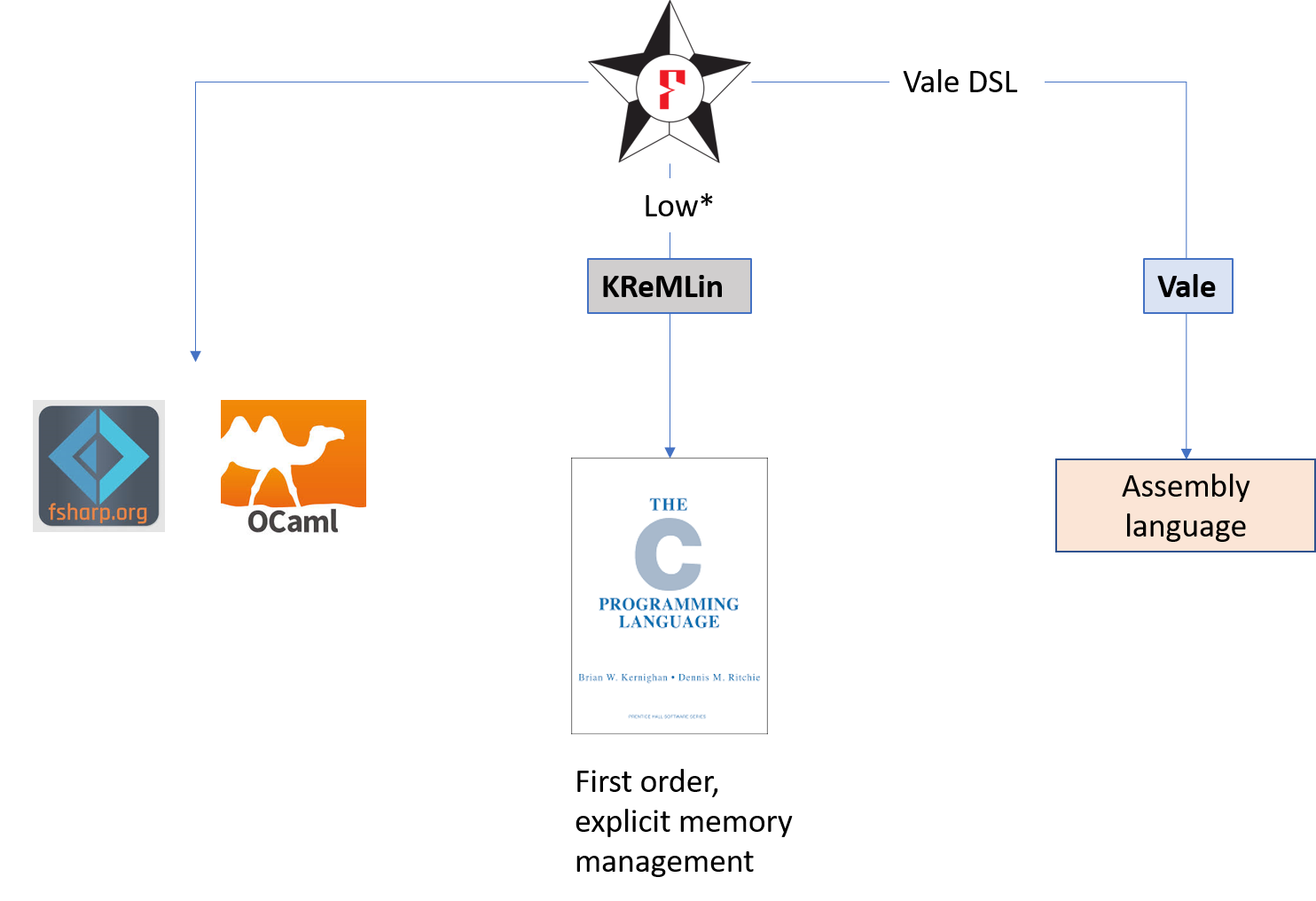
The Functional Core of F*
Informally, like Coq or Agda, but with an extensional type theory (~Nuprl)
-
Refinement types
let nat = x:int{x>=0} -
Recursive functions
let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1))
Refinement types
type nat = x:int{x>=0}-
Refinements introduced by type annotations (code unchanged)
let rec factorial (n:nat) : nat = if n = 0 then 1 else n * (factorial (n - 1)) -
Logical obligations discharged by SMT (simplified)
n >= 0, n <> 0 |= n - 1 >= 0 n >= 0, n <> 0, factorial (n - 1) >= 0 |= n * (factorial (n - 1)) >= 0 -
Refinements eliminated by subtyping:
nat<:intlet i : int = factorial 42 let f : x:nat{x>0} -> int = factorial
Dependent types
-
Dependent function types (), here together with refinements:
val incr : x:int -> y:int{x < y} let incr x = x + 1 -
Can express pre- and post- conditions of pure functions
val incr : x:int -> y:int{y = x + 1} -
Exercise: Can you find other types for
incr?
Inductive types and pattern matching
-
Inductive datatypes (immutable) and pattern matching
type list a = | Nil : list a | Cons : hd:a -> tl:list a -> list a let rec map (f:a -> b) (x:list a) : list b = match x with | [] -> [] | h :: t -> f h :: map f t -
Lambdas (unnamed, first-class functions)
map (fun x -> x + 42) [1;2;3]
Inductive types and pattern matching
-
Recursive functions over inductive datatypes
type vec a : nat -> Type = | Nil : vec a 0 | Cons : #n:nat -> hd:a -> tl:vec a n -> vec a (n + 1) let rec append (v1:vec a n) (v2:vec a m) : vec a (n + m) = match v1 with | Nil -> v2 | Cons hd tl -> Cons hd (append tl v2) -
Higher order
let rec map (f:a -> b) (v:vec a n) : vec b n = match v with | Nil -> Nil | Cons hd tl -> Cons (f hd) (map f tl) map (fun x -> x + 42) (Cons 1 Nil)
Total functions in F*
-
The F* functions we saw so far were all total
-
Toteffect (default) = no side-effects, terminates on all inputsa -> bis really shorthand fora -> Tot b
val factorial : nat -> nat ~ nat -> Tot nat let rec factorial n = (if n = 0 then 1 else n * (factorial (n - 1))) -
Quiz: How about giving this weak type to factorial?
val factorial : int -> Tot int
let rec factorial n = (if n = 0 then 1 else n * (factorial (n - 1)))
^^^^^
Subtyping check failed; expected type (x:int{(x << n)}); got type int factorial (-1) loops! (int type in F* is unbounded)
Semantic termination checking
- Based on well-founded ordering on expressions (
<<)- naturals related by
<(negative integers unrelated) - inductives related by subterm ordering
- lex tuples
%[a;b;c]with lexicographic ordering - result of a total function smaller than the function itself (
f x << f)
- naturals related by
- order constraints discharged by the SMT solver
- arbitrary total expression as decreases metric
let rec ackermann (m n:nat) : Tot nat (decreases %[m;n]) = if m=0 then n + 1 else if n = 0 then ackermann (m - 1) 1 else ackermann (m - 1) (ackermann m (n - 1)) - default metric is lex ordering of all (non-function) args
val ackermann: m:nat -> n:nat -> Tot nat
Values and Computations
-
“Values” aka unconditionally total terms
-
Two classes of types
- Value types (
t):int,list int, … - Computation types (
C): conditionally pure, divergent, stateful, …
- Value types (
-
F* effect system encapsulates effectful code
- Pure code cannot call effectful code
- But, via sub-effecting, pure code can be used in effectful contexts
-
Dependent function types of the form:
x:t -> C- F* is call-by-value
- argument can't have side-effects, so value type
-
Two forms of refinement types
- Refined value types:
x:t{p} - Refined computation types …
- Refined value types:
Refined Computation Types
Refined Computation Types
-
Saw this already:
val factorial : nat -> Tot nat -
Can equivalently use pre- and post- conditions for this
val factorial : x:int -> Pure int (requires (x >= 0)) (ensures (fun y -> y >= 0)) -
Each computation type contains
- effect (
Pure), result type (int), spec (e.g. pre and post)
- effect (
-
Totcan be seen as just an abbreviationTot t = Pure t (requires True) (ensures (fun _ -> True))
Intrinsic vs Extrinsic Proofs
-
Intrinsic proof: The type of a term at the “definition site” expresses properties of interest
let rec factorial (n:nat) : Tot nat = if n = 0 then 1 else n * factorial (n - 1) - Extrinsic proof: The type of a term is relatively simple; properties are proven separately from the definition
Lemma: Pure Computations as Extrinsic Proofs
let rec append (#a:Type) (xs ys : list a) : Tot (list a) =
match xs with
| [] -> ys
| x :: xs' -> x :: append xs' yslet rec append_length (#a:Type) (xs ys : list a) :
Pure unit
(requires True)
(ensures (fun _ -> length (append xs ys) = length xs + length ys))
= match xs with
| [] -> ()
| x :: xs' -> append_length xs' ys- Syntax sugar (
Lemma)let rec append_length_lemma (#a:Type) (xs ys : list a) : Lemma (ensures (length (append xs ys) = length xs + length ys)) = match xs with | [] -> () | x :: xs' -> append_length_lemma xs' ys
Often lemmas are unavoidable
let snoc l h = l @ [h]
let rec reverse (#a:Type) (l:list a) : Tot (list a) =
match l with
| [] -> []
| hd::tl -> snoc (reverse tl) hdlet rec rev_snoc #a (l:list a) (h:a)
: Lemma (reverse (snoc l h) == h::reverse l) =
match l with
| [] -> ()
| hd::tl -> rev_snoc tl hlet rec rev_involutive #a (l:list a)
: Lemma (reverse (reverse l) == l) =
match l with
| [] -> ()
| hd::tl -> rev_involutive tl; rev_snoc (reverse tl) hdVerifying pure programs
Variant #3: extrinsically using proof terms
let rec preservation (#e #e':exp) (#g:env) (#t:typ)
(ht:typing g e t)
(hs:step e e')
: Tot (typing g e' t) (decreases ht) =
match hs with
| SBeta tx e1' e2' -> substitution_beta h2 (TyLam?.hbody h1)
| SApp1 e2' hs1 -> TyApp (preservation h1 hs1) h2
| SApp2 e1' hs2 -> TyApp h1 (preservation h2 hs2)let rec progress (#e:exp) (#t:typ)
(h:typing empty e t)
: Pure (e':exp & step e e')
(requires (~ (is_value e)))
(ensures (fun _ -> True)) (decreases h) =
match h with
| TyApp #g #e1 #e2 #t11 #t12 h1 h2 ->
match e1 with
| ELam t e1' -> (| subst (sub_beta e2) e1', SBeta t e1' e2 |)
| _ -> let ExIntro e1' h1' = progress h1 in
(| EApp e1' e2, SApp1 e2 h1' |)a- Note: match exhaustiveness check also semantic (via SMT)
